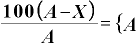 ・
・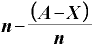 ・
・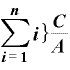
「損益がゼロになる償還時レート」を求めてみる
【考え方】
損益がゼロになるのは、
償還時の為替差損のマイナス分=受け取る利払い分合計 ……(1)
となる為替レート。
その償還時レートをXとして、(1)の等式を立てて、その等式をXについて解けば出てくる。
当初レート:A
償還時レート:X
利払い回数合計:n
クーポン:C
とすると、(1)の等式は、
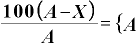 ・
・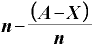 ・
・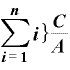
これをXについて解いてみる。
【解き方・途中式】
両辺に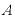 を掛ければ、両辺の
を掛ければ、両辺の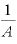 が消える。
が消える。
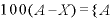 ・
・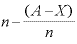 ・
・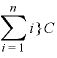
カッコを開いて、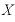 関連の項を取りあえず右辺に、それ以外は左辺に移項する。
関連の項を取りあえず右辺に、それ以外は左辺に移項する。
「Σ」は単に「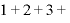 ……
……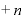 」を略したマークなので、「ひとつの数」的なものとして扱ってOK。
」を略したマークなので、「ひとつの数」的なものとして扱ってOK。
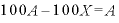 ・
・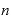 ・
・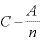 ・
・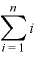 ・
・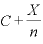 ・
・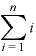 ・
・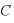
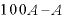 ・
・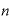 ・
・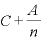 ・
・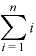 ・
・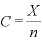 ・
・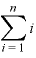 ・
・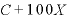
両辺の「n分の1」が少々うざいので、ここで、両辺にnを掛けておく。
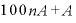 ・
・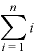 ・
・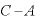 ・
・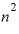 ・
・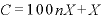 ・
・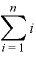 ・
・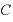
左辺はAについて、右辺はXについてまとめる。
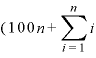 ・
・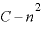 ・
・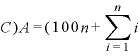 ・
・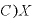
右辺のカッコ内「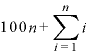 ・
・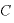 」で両辺を割れば(つまり、「
」で両辺を割れば(つまり、「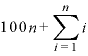 ・
・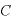 」左辺の分母に持ってくれば)、「X=」の式になる。
」左辺の分母に持ってくれば)、「X=」の式になる。
X=を左辺すると、
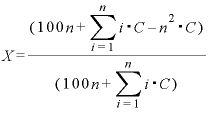 ・
・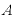
ここで、分母の「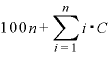 」が
分子にもあることに注目。
」が
分子にもあることに注目。
分子を「(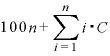 )
)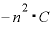 」と考えて、上式をまとめると、
」と考えて、上式をまとめると、
償還時レート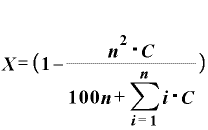 ・
・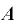
となります。◇