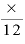 」年とします。3年3ヶ月であれば「3+
」年とします。3年3ヶ月であれば「3+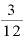 」で3.25年、5年10ヶ月なら「5+
」で3.25年、5年10ヶ月なら「5+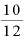 」で5.833…年です。
」で5.833…年です。「0.5乗」とは一体どういう意味なのか
■指数の数字を細かく変えればありとあらゆる数が表現できる■
本書巻末の「債券の仕組み」の中にも少し書いていますが、金利計算では期間(年数T)は厳密には日数を年換算した値を用います。
概算で「約○年×ヶ月」とする場合には、「○+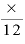 」年とします。3年3ヶ月であれば「3+
」年とします。3年3ヶ月であれば「3+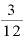 」で3.25年、5年10ヶ月なら「5+
」で3.25年、5年10ヶ月なら「5+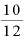 」で5.833…年です。
」で5.833…年です。
高校の数Ⅱで指数関数をやったときには、2乗とか5乗とか、「何乗」の指数部分は整数のケースがほとんどだったと思いますが、「何乗」の部分が整数と決まっているわけではありません。
複利の計算期間のように、3.25乗なり、5.833乗なり、「小数点がついた数」や「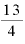 乗」や「
乗」や「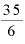 乗」のように「分数」が指数になることもあるわけです。
乗」のように「分数」が指数になることもあるわけです。
加えて、「マイナス5乗」「マイナス4.85乗」「マイナス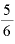 乗」というふうに、「負の数」乗の値もあります。
乗」というふうに、「負の数」乗の値もあります。
(ちなみに、債券の価格計算では、この「負の数」乗を頻繁に使います。)
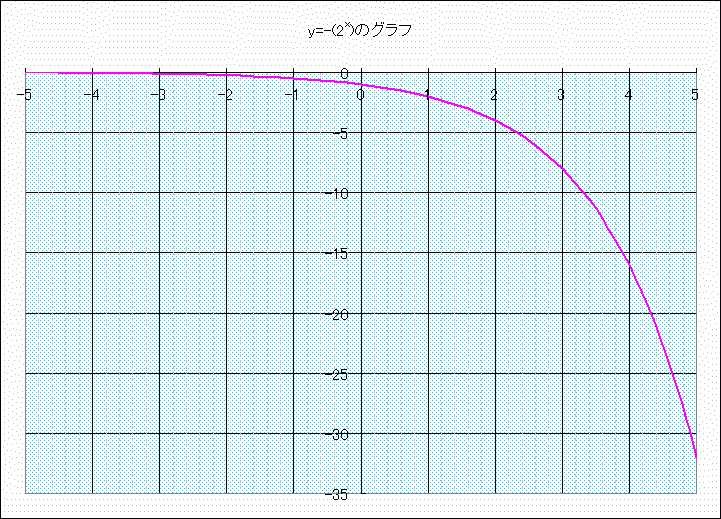
「小数点のついた数」乗や「分数」乗、「負の数」乗をもう少し詳しく知るために、ここで、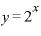 という指数関数のグラフを見てみます。
という指数関数のグラフを見てみます。
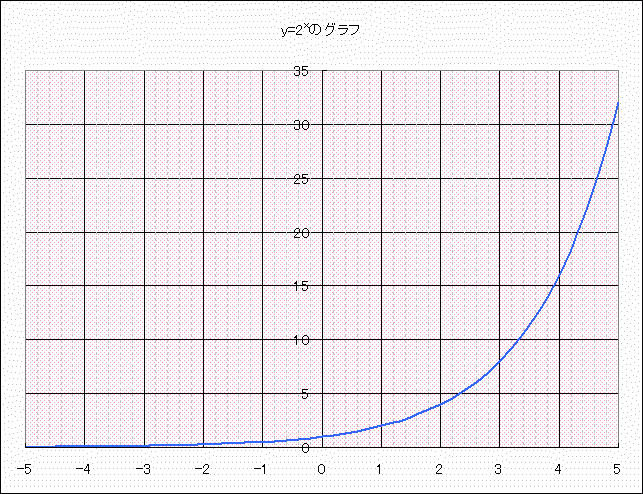
このグラフは、xの範囲が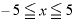 で、それに対応するyの範囲は「
で、それに対応するyの範囲は「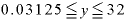 」となっています。
」となっています。
グラフの線が途切れることなく連続しているということは、xの値を細かく変えれば yの値として「
yの値として「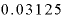 から32までの、ありとあらゆる数(実数)が表現できることを意味します。
から32までの、ありとあらゆる数(実数)が表現できることを意味します。
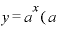 >
1の定数)の指数関数の場合、指数部分のxの値のマイナスが大きくなるほど、yの値はゼロに近づいていきます。
>
1の定数)の指数関数の場合、指数部分のxの値のマイナスが大きくなるほど、yの値はゼロに近づいていきます。
ですから、xの範囲を-∞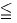 x
x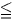 ∞とすれば、xの値を細かく変えることで、yの値として「0
∞とすれば、xの値を細かく変えることで、yの値として「0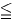 y
y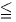 ∞」のありとあらゆる数が表現できるわけです。
∞」のありとあらゆる数が表現できるわけです。
また、たとえば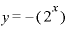 とすれば、xの値を細かく変えていくことによって、yの値として「
とすれば、xの値を細かく変えていくことによって、yの値として「 -∞」のありとあらゆる数が表現できます。
-∞」のありとあらゆる数が表現できます。
つまり、「小数点がついた数」乗、あるいは「分数」乗といった指数を使えば、細かな期間(日数まで年換算した「年数T」)に対応する複利の元利合計額が計算できる、というわけです。
なお、指数関数の底はゼロより大きく、かつ、1でない数であることが条件となっています。
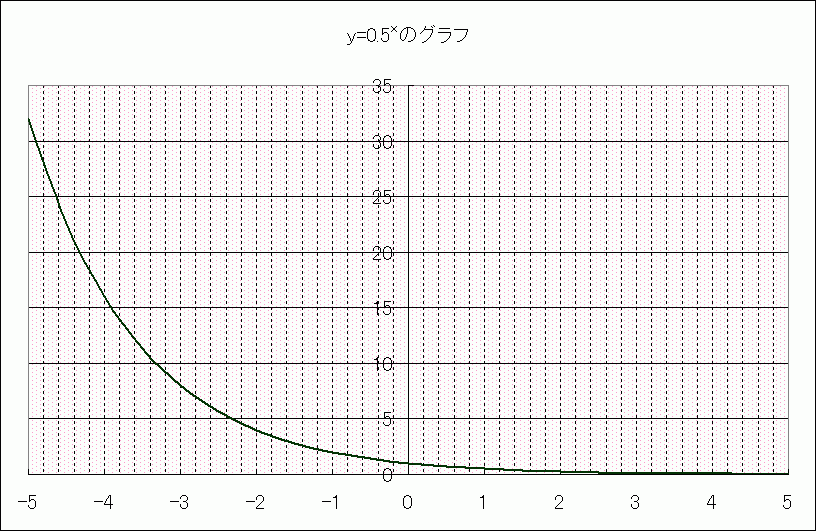
上で見たグラフは「2のx乗」のグラフで、底が1より大きい数の指数関数のグラフはこのような形になりますが、底が「0より大きく、1より小さい」場合には、グラフの形は下のようになります。
■「2の3乗」は2×2×2。では、「2のマイナス5乗」とは何か■
ところで、たとえば「2の3乗」と言えば「2×2×2」で2を3回掛ける、「2の5乗」なら「2×2×2×2×2」で2を5回掛けるということはわかります。
しかし、「2の0.5乗」というのは何なのか。「2を0.5回掛ける」とは、どんな意味なのでしょうか。
あるいは、「2の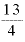 乗」とは、「2」という数をどうすることなのか。ましてや、「2のマイナス5乗」といった負の数乗の数字とは何なのでしょうか。
乗」とは、「2」という数をどうすることなのか。ましてや、「2のマイナス5乗」といった負の数乗の数字とは何なのでしょうか。
これらが何を示すものか具体的に理解するために、ここで数Ⅱで習った「指数法則」を思い出してみましょう。
(指数法則その1)…底が同じ数の掛け算は、指数部分の数の足し算で表現できる。
たとえば、「2の2乗」×「2の3乗」であれば、「2の(2+3=)5乗」になる、という法則。
なぜ、もともと掛け算であったものを「指数部分の足し算」にしてしまってよいかというと、「2の2乗」は2を2回掛けたもの、「2の3乗」は2を3回掛けたものなので、
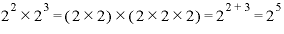
となるからです。
底の値はゼロより大きい数ならば何でもよくて、これを「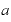 」という文字で、指数を「
」という文字で、指数を「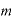 」「
」「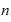 」という文字で表すとすれば、
」という文字で表すとすれば、
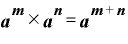
となります。
(指数法則その2)…底が同じ数の割り算は、指数部分の数の引き算で表現できる。
たとえば、「2の5乗」÷「2の3乗」であれば、「2の(5-3=)2乗」になる、という法則。
指数部分の引き算になる理由は、指数法則その1と同じように考えればすぐにわかると思います。
「2の5乗」は2を5回掛けたもので、これを「2の3乗」すなわち2を3回掛けたもので割るということは、、
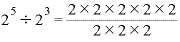
という分数になります。
分母にある「2」の個数分、分子の「2」が約分できて消えるので、
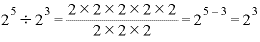
となるわけです。
これも底を「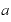 」、指数の数を「
」、指数の数を「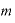 」「
」「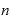 」として表すと、
」として表すと、
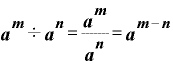
です。
と、このように、指数がついている数というのは、「掛け算を足し算として計算できる」「割り算を引き算として計算できる」という、とても便利なものなのです。
ここで、指数法則その2を今一度見てください。
この法則で、2つの数の指数部分の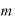 と
と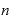 が同じ数だとしたらどうなるでしょうか。つまり「
が同じ数だとしたらどうなるでしょうか。つまり「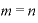 」というケースです。
」というケースです。
指数部分を引き算すると、「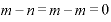 」と、指数部分がゼロになってしまいます。底が2ならば「2のゼロ乗」、底を「
」と、指数部分がゼロになってしまいます。底が2ならば「2のゼロ乗」、底を「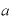 」とするならば、「
」とするならば、「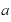 のゼロ乗」です。
のゼロ乗」です。
「ゼロ乗」とは、何でしょうか。
指数法則その2を逆から考えていくと、
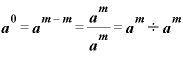
になります。
「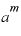 を
を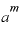 で割る」という、ある数を同じ数で割るわけですから、答えは「1」です。
で割る」という、ある数を同じ数で割るわけですから、答えは「1」です。
つまり、底がゼロより大きいどんな数であっても、「ゼロ乗」といったら、それは「1」なのです。
そこで、
(指数法則その3)…底がいくらであっても、「ゼロ乗」のときは1.
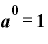
です。
単利と複利の計算では、「スタート地点(T=0)はどちらも同じ元本金額そのもの」でした。最初から同じ元本金額を想定しているのだから当然といえば当然なのですが、これは、年数Tがゼロの場合、
(単利の式) 元本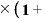 (金利)
(金利)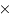 0)=元本
0)=元本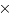 1=元本そのもの
1=元本そのもの
(複利の式) 元本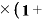 金利
金利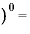 元本
元本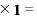 元本そのもの
元本そのもの
という計算の結果でもあります。
この指数法則その3を踏まえたうえで、もう一度、指数法則その2を見てみます。
もし、指数部分の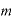 が0、
が0、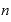 が0でない数、たとえば「5」だとしたら、これはどういう数になるでしょうか。
が0でない数、たとえば「5」だとしたら、これはどういう数になるでしょうか。
指数の部分は「0-5」で-5となります。
底が「2」の場合ならば、
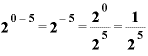
です。
「2のマイナス5乗」というのは、「2の5乗分の1」という、2の5乗の逆数だったのです。
底が2でなくても同じです。
指数部分が「マイナス何乗」となっている数とは、「(底の)何乗分の1」という逆数を表します。
そこで、
(指数法則その4)…「マイナス何乗」は「何乗分の1」を表す。
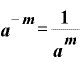
となります。
これで、「マイナス何乗」という数が何を表すのかがわかりました。
■「2を0.5回分掛けた数」とはどんな数?■
今度は「小数点がついた数」乗、「分数」乗の数を考えてみます。
まず
(指数法則その5)…指数がついた数をさらに何乗かした数は、指数部分の掛け算で表現できる。
たとえば、「2の3乗」をさらに2乗した数は、「2の(3×2=)6乗」になる、といった具合です。
「2の3乗」をさらに2乗するというのは、
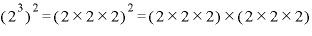
と、「3乗」の部分が2倍になります。なぜ2倍かといえば、「2乗」するからにほかなりません。これが4乗であれば、「2の3乗」を4回掛けることになるので、「2の(3×4=)12乗」です。
底を「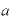 」、指数部分を「
」、指数部分を「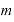 」「
」「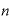 」として表せば、
」として表せば、
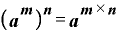
というわけです。
この指数部分の「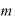 」や「
」や「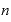 」ですが、この数は0であっても、マイナスであっても、小数であっても、分数であっても、どんな数でも構いません。
」ですが、この数は0であっても、マイナスであっても、小数であっても、分数であっても、どんな数でも構いません。
ここで、mが0.5の場合を考えてみます。
m=0.5だとすると、nが2のときm×nは「0.5×2」で1となります。
底が「2」だとすると、
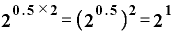
です。
「2の1乗」は「2」そのものです。つまり、この式は、「『2の0.5乗』なる数を2乗すると『2』になる」ことを表しています。
ということは、「2の0.5乗」なる数は、「それを2乗すると2になる数」ということになります。
その数は何かといえば、そうです。「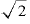 」、です。
」、です。
「2を0.5乗(=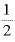 乗)する」、「2を0.5回(=
乗)する」、「2を0.5回(=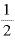 回)掛ける」というのは「2乗して(底である)2にする」ということだったわけです。
回)掛ける」というのは「2乗して(底である)2にする」ということだったわけです。
ここで金利の計算のことを思い出すと、金利が4%で、期間が0.5(=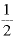 )年のときの複利計算の式は(
)年のときの複利計算の式は(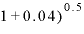 でした。この式から出てくる数は、「2乗すると1.04になる数」を意味します。それが「1.0198」という値です。
でした。この式から出てくる数は、「2乗すると1.04になる数」を意味します。それが「1.0198」という値です。
では、2の「3分の1乗」はどうでしょうか。
これは「3乗すると2になる数」ということですから、これは「2の3乗根」、![\sqrt[3]{2} \sqrt[3]{2}](./110308a_images/math064.png) です。
です。
そこで、
(指数法則その6)…「○分の1乗」は「○乗根」を表す。
底が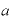 の場合、
の場合、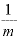 乗は
乗は
![\bm{a}^{\frac{\bm{1}}{\bm{m}}}=\sqrt[\bm{m}]{\bm{a}} \bm{a}^{\frac{\bm{1}}{\bm{m}}}=\sqrt[\bm{m}]{\bm{a}}](./110308a_images/math067.png)
です。
指数部分が「4分の3乗」や「12分の7乗」など、「分子が1でない分数」乗の場合はどんな数になるかというと、これも指数法則その5と指数法則その6から考えることができます。
たとえば、「12分の7乗」という数は「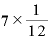 」です。
」です。
底をaとして、指数法則その5を逆から用いれば
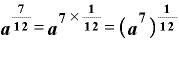
という形になります。
つまり、「12分の7乗」とは、「底を7乗したものの12乗根」という意味です。√を使って表せば、
![\bm{a}^{\frac{\bm{7}}{\bm{1}\bm{2}}}=\bm{(}\bm{a}^{\bm{7}}\bm{)}^{\frac{\bm{1}}{\bm{1}\bm{2}}}=\sqrt[\bm{1}\bm{2}]{\bm{a}^{\bm{7}}} \bm{a}^{\frac{\bm{7}}{\bm{1}\bm{2}}}=\bm{(}\bm{a}^{\bm{7}}\bm{)}^{\frac{\bm{1}}{\bm{1}\bm{2}}}=\sqrt[\bm{1}\bm{2}]{\bm{a}^{\bm{7}}}](./110308a_images/math070.png)
となります。
ちなみに、「12分の7」を「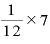 」として考えれば、これは「底を12乗根したものを7乗した数」とも捉えられます。式に表せば、
」として考えれば、これは「底を12乗根したものを7乗した数」とも捉えられます。式に表せば、
![\bm{a}^{\frac{\bm{7}}{\bm{1}\bm{2}}}=\bm{(}\bm{a}^{\frac{\bm{1}}{\bm{1}\bm{2}}}\bm{)}^{\bm{7}}=\bm{(}\sqrt[\bm{1}\bm{2}]{\bm{a}}\bm{)}^{\bm{7}} \bm{a}^{\frac{\bm{7}}{\bm{1}\bm{2}}}=\bm{(}\bm{a}^{\frac{\bm{1}}{\bm{1}\bm{2}}}\bm{)}^{\bm{7}}=\bm{(}\sqrt[\bm{1}\bm{2}]{\bm{a}}\bm{)}^{\bm{7}}](./110308a_images/math072.png)
と書けます。
これらをまとめて、
(指数法則その7)…「○分の×乗」は、「×乗したものの○乗根」または「○乗根を×乗した数」を表す。
底がaのとき、「m分のn乗」は、
![\bm{a}^{\frac{\bm{n}}{\bm{m}}}=\sqrt[\bm{m}]{\bm{a}^{\bm{n}}}=\bm{(}\sqrt[\bm{m}]{\bm{a}}\bm{)}^{\bm{n}} \bm{a}^{\frac{\bm{n}}{\bm{m}}}=\sqrt[\bm{m}]{\bm{a}^{\bm{n}}}=\bm{(}\sqrt[\bm{m}]{\bm{a}}\bm{)}^{\bm{n}}](./110308a_images/math073.png)
と表現できます。◇