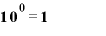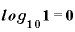
こんなときには「対数グラフ」が見やすい

■「10倍の数値ごと」に目盛りが等間隔■

本文で、金利をｘ軸に、「元本が２倍になる年数」をｙ軸にとったグラフを紹介しています。

このグラフの形態は「対数グラフ」と呼ばれるもので、データの値の幅が非常に大きいときに用いられます。

通常のグラフとの違いは、目盛りの間隔です。

通常のグラフの目盛りは、１、２、３…という目盛りの間隔は同じです。

０～10の目盛りの間隔は、1０～20の目盛りの間隔や、20～30の目盛りの間隔と同じわけですが、対数グラフでは、１～10の目盛り間隔と同じになるのは、10～100の目盛り間隔、100～1000の目盛り間隔、といった具合に、数値が10倍になるごとに目盛りが等間隔になります。

そこで使われているのが常用対数、すなわち、底が10の対数です。

常用対数は「10の何乗か」を表す値です。

　　　　　　 $\bm{1}\bm{0}^{\bm{0}}=\bm{1}$ →　　 $\bm{l}\bm{o}\bm{g}_{\bm{1}\bm{0}}\bm{1}=\bm{0}$

$\bm{1}\bm{0}^{\bm{1}}=\bm{1}\bm{0}$ →　　 $\bm{l}\bm{o}\bm{g}_{\bm{1}\bm{0}}\bm{1}\bm{0}=\bm{1}$

$\bm{1}\bm{0}^{\bm{2}}=\bm{1}\bm{0}\bm{0}$ →　　 $\bm{l}\bm{o}\bm{g}_{\bm{1}\bm{0}}\bm{1}\bm{0}\bm{0}=\bm{l}\bm{o}\bm{g}_{\bm{1}\bm{0}}\bm{1}\bm{0}^{\bm{2}}=\bm{2}$

$\bm{1}\bm{0}^{\bm{3}}=\bm{1}\bm{0}\bm{0}\bm{0}$ →　　 $\bm{l}\bm{o}\bm{g}_{\bm{1}\bm{0}}\bm{1}\bm{0}\bm{0}\bm{0}=\bm{l}\bm{o}\bm{g}_{\bm{1}\bm{0}}\bm{1}\bm{0}^{\bm{3}}=\bm{3}$

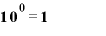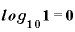
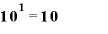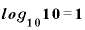
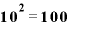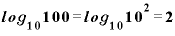
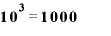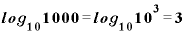
というふうになりますから、１という値はグラフ上では目盛り「０」のところに、10という値は目盛り「１」、100は目盛り「２」のところにきます。

そうすると、通常のグラフと同じ目盛りの数でも非常に大きな数まで表示することができます。

たとえば、データの値が０から1000の範囲内にあったとすると、１目盛りの単位を10に取ると１００目盛り分が必要です。１目盛りを１００にすれば10目盛り分で済みますが、１目盛り分が大きすぎれば、今後は細かなグラフの推移が見えにくくなってしまいます。

対数グラフならば、０から１０００までの範囲内のデータは３目盛り分で済んでしまいます。

さらに、その目盛り間に補助目盛りを入れれば、グラフの推移の細かな推移も見えます。

本文で紹介している「金利」と「元本が２倍になる年数」の場合、金利が0.01％で元本が２倍になるには6931年もかかります。

それが、金利が１％ならば69.66年と、この0.01％から１％までの間の年数は約100倍も違ってきます。

金利が10.5％ともなれば、元本が２倍になる年数は７年弱と、0.01％と比べると1000倍もの差です。

これを通常のグラフで表すと、金利が非常に低いところだけが値が異常に大きく、金利１％以降はもはやｘ軸に張り付いているようにしか見えません。

このような場合、対数グラフにすると、本文にも掲載した描写になり、変化の様子が見やすくなります。

■飛躍的に伸びる業績や株価も対数グラフで■

たとえば「１だったものが10になった」という場合、通常のグラフはこれを「１から９増えて10になった」という表し方をします。

対数グラフでは、これを「10倍になった」として扱います。

「１が10になった」を、「９増えた」と受け取るか、「10倍になった」と受け取るかは、取り扱う対象の性質にもよります。

たとえば、元本10万円を10年で１００万円に増やしたとしましょう。金額ベースではプラス90万円、率でいうと、1000％（10倍）の運用です。

その100万円を次の10年で190万円に増やしたとします。金額ベースでは同じプラス90万円ですから、「最初の10年と同じペースで増やした」ということになります。

しかし、率で考えると190％（1.9倍）と、、最初の10年の運用と比べるとガタ落ちです。「元本を10倍に増やした」という、最初の10年と同等の運用というのであれば、100万円を10年で1000万円にしてこそだろう、とも言えるわけです。

企業の業績や株価なども、同じような考え方ができます。

たとえば、当初200円だった株価が５年後に1000円に上昇したとします。価格的にはプラス800円、伸び率で言うと500％（５倍）です。

次の５年で株価が1800円になった場合、価格的には「同じペースの上昇」ですが、伸び率は180％（1.8倍）と大幅に落ちます。

もし、当初から５年の株価上昇力が維持されているのであれば、1000円の株価は5年後には5000円になっているはずで、それが1800円でしかないのは、上昇力が鈍っている、と解釈することも可能です。

そうした観点で業績や株価の推移を捉える意味で、とくに長期的なデータを見る場合には、対数グラフにしてみるのもよいと思います。

下の２つのグラフは、どちらもＮＹダウの1928年10月１日から2011年４月１日までの株価チャートです。

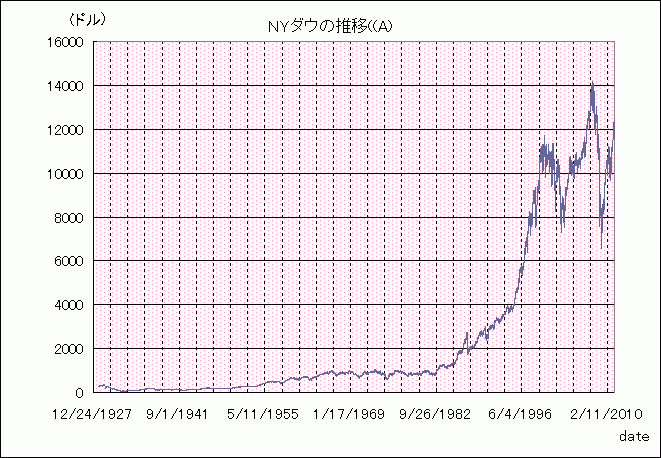
当初240ドルだった株価は2011年４月初めには1万2376.72ドルにまで上昇していて、これを通常のチャートにすると、Ａのような形になります。

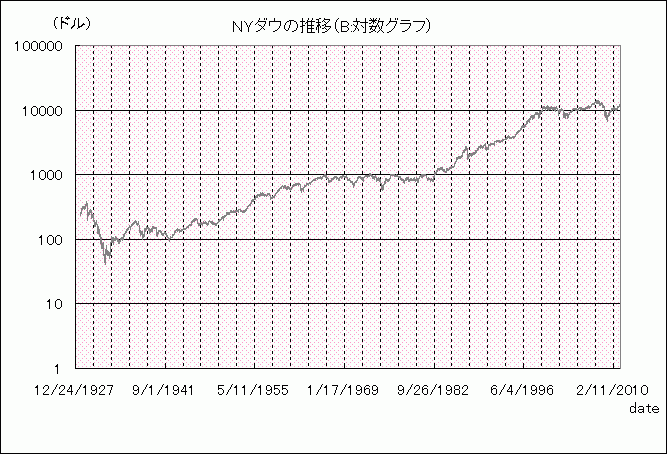
これを見ると、「90年代に入ってからものすごい上昇」であり、「ここ数年は、ものすごい乱高下」という印象ですが、これを対数グラフにするとＢのようになります。

Ｂを見ると、伸びに勢いがあったのは82年から2000年辺りにかけてまでで、その後は「もみ合い」のような格好です。2000年以降の推移は、60年代後半から80年代初頭にかけての動きにも似ています。

60年代後半から80年代初頭といえば、米国経済は停滞していた時期、これに対して2000年代の米国経済は、”9.11”や”リーマンショック”で激しく落ち込む局面はあったもののその間には非常に強い拡大局面がありました。

この２つの時期の株価の推移が、対数グラフで見ると似ているというのは、興味深いところでもあります。

と、いうふうに、長期的なデータを対数グラフ化してみると、通常のグラフでは思いつかない視点も浮かんできたりします。

一度試してみてはどうでしょうか。　　◇