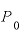「元本が２倍になる年数」＝「元本が半減する年数」の理由

元本が２倍に増える年数と、マイナス運用によって元本が半分に減ってしまう年数が同じ、というのは、感覚的にも「それはそうだろう」と思うところでしょう。

このことは式で表すことができます。

ここでは２つの考え方を紹介します。

＜その１＞「半分」を「２倍の『マイナス１乗』」と捉える

（１＋金利ｒ）をＲという一文字に置き換えると、元利合計額が元本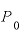 $P_{0}$ の２倍になる年数Ｔは、本文の中でも紹介しているように、

　　　　　　 $\bm{2}=\bm{R}^{\bm{T}}$

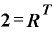
という式になります。

年数Ｔを表す対数は、

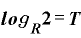　　　　　　 $\bm{l}\bm{o}\bm{g}_{\bm{R}}\bm{2}=\bm{T}$ 　　　　　……（Ａ）

です。

一方、マイナス複利運用で元本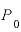 $P_{0}$ が半分になる年数Ｔは、

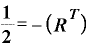　　　　　　 $\displaystyle \frac{\bm{1}}{\bm{2}}=-\bm{(}\bm{R}^{\bm{T}}\bm{)}$ 　　　　……（Ｂ）

で表されます。

ここで、指数法則の中の

　　　　　　 $\displaystyle \bm{a}^{-\bm{m}}=\frac{\bm{1}}{\bm{a}^{\bm{m}}}$

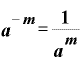
「ある数のマイナスｍ乗は、『ある数のｍ乗』分の１である」を使ってみると、「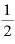 $\displaystyle \frac{1}{2}$ 」という数字は「『２の１乗』分の１」ですから、「２のマイナス１乗」ということになります。

これを用いると、（Ｂ）式は

　　　　　　 $\displaystyle \frac{\bm{1}}{\bm{2}}=\bm{2}^{-\bm{1}}=-\bm{(}\bm{R}^{\bm{T}}\bm{)}$

　　　　　 $-\bm{(}\bm{2}^{-\bm{1}}\bm{)}=\bm{R}^{\bm{T}}$

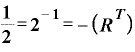
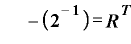
という表現に変わります。。

これを、年数Ｔを表すという対数の形にすると、

　　　　　　 $-\bm{l}\bm{o}\bm{g}_{\bm{R}}\bm{2}^{-\bm{1}}=\bm{T}$

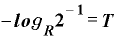
です。

さらに、対数の公式に出てきた

　　　　　　 $\bm{l}\bm{o}\bm{g}_{\bm{a}}\bm{b}^{\bm{n}}=\bm{n}$ ・ $\bm{l}\bm{o}\bm{g}_{\bm{a}}\bm{b}$

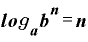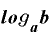
「真数がｎ乗になっている場合は、真数部分から『ｎ乗』を取り外した対数と『ｎ』の掛け算にできる」を使うと、

　　　　　　 $-\bm{l}\bm{o}\bm{g}_{\bm{R}}\bm{2}^{-\bm{1}}=\bm{(}-\bm{1}\bm{)}$ ・ $\bm{(}-\bm{l}\bm{o}\bm{g}_{\bm{R}}\bm{2}\bm{)}=\bm{l}\bm{o}\bm{g}_{\bm{R}}\bm{2}=\bm{T}$

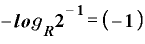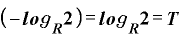
で、（Ａ）式と同じになります。　　　◇

＜その２＞「Ｔ年前、元本は今の元利合計額の２倍だった」と考える

「いまの元利合計額Ｐが、かつての元本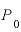 $P_{0}$ の半分」ということは、逆から言えば「元本 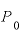$P_{0}$ はいまの元利合計額Ｐの２倍である」ということでもあります。

　　　　　　 $P_{0}=2P$

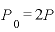
です。

そうすると、「いまの元利合計額Ｐは、（１＋金利ｒ）でマイナス運用したら、Ｔ年後に元本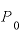 $P_{0}$ の半分になっている」は、「（１＋金利ｒ）でマイナス運用されてきた、いまの元利合計額ＰをＴ年前に遡ると、それは、いまの元利合計額の２倍『２Ｐ』であった」という言い方もできます。

これを式にすると、

　　　　　　 $\bm{P}_{\bm{0}}=\bm{2}\bm{P}=\bm{P}$ ・ $\bm{\{}-\bm{(}\bm{R}^{-\bm{T}}\bm{)}\bm{\}}$

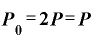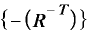
となります。「マイナスＴ乗」というのが、「Ｔ年前に遡る」を意味します。

これを、「Ｔ年前」を表す対数にすると、

　　　　　　 $\bm{2}=-\bm{(}\bm{R}^{-\bm{T}}\bm{)}$

$-\bm{2}=\bm{R}^{-\bm{T}}$

$-\bm{l}\bm{o}\bm{g}_{\bm{R}}\bm{2}=-\bm{T}$

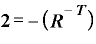
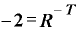
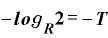
となります。両辺のマイナスですから、これを取ってｓまうと、

　　　　　　 $\bm{l}\bm{o}\bm{g}_{\bm{R}}\bm{2}=\bm{T}$

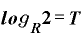
と、やはり（Ａ）式と同じになります。　　　◇