「半減期」の超基礎知識
■放射性崩壊で一定周期ごとに原子核の残存数が半分になる■
自然界に存在する元素の中には、同じ元素でありながら中性子の数が異なるものがあります。たとえば、通常の炭素(炭素12)の原子核は陽子が6、中性子6ですが、たまに陽子数は同じ6でも中性子の数が8つあるもの(炭素14)が存在しています。
このような物質は同位体と呼ばれます。
同位体には、構造が安定的でそのまま存在し続けているものと、不安定なために自ずと崩壊してしまい、安定した別の物質の原子核になってしまうものとがあります。
ある原子核が崩壊して別の原子核になるときには放射線を発します。放射線を出しながら崩壊するので、これを放射性崩壊、そうした同位体は放射性同位体と呼ばれます。
ちなみに、この放射線には、ヘリウム(α崩壊)、電子(β崩壊)、電磁波(γ崩壊)の3種類があります。
あるまとまった数の原子核があって、それが放射性崩壊して別の物質になると、もとの原子核の数は減ってしまいます。
となると、その原子核はあるとき全く存在しなくなってしまいそうですが、実際にはそうはなっていません。
というのは、どの原子核も「ある時期がくると一斉に崩壊してなくなる」のではなく、とある原子核はすぐに崩壊するけれども、別の原子核はなかなか崩壊しない、というふうに、個別の原子核で崩壊するまでの時間が異なるからです。
そうすると、原子核の数は、崩壊が始まってから、徐々に、じわじわ減っていく格好になります。
徐々に、じわじわ減っていって、もとの原子核の数が半分になるまでに要する時間が「半減期」です。
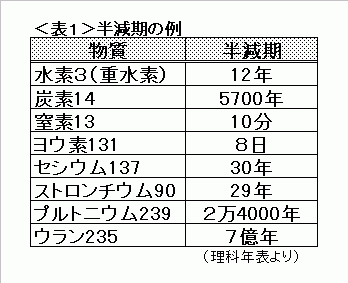
物質ごとの半減期の長さは、先人の研究で明らかになっています。

たとえば、福島原発の放射性物質飛散の問題でよく採り上げられるヨウ素131は、半減期が8日です。
半減期が8日ということは、崩壊が始まって8日後には半分なくなり、16日後にはもうヨウ素131は存在しなくなる、というような感じがするかもしれませんが、そうはなりません。
もとの原子核の数が1000の場合、8日後には半分の500になり、16日後にはそのまた半分の250に、24日後にはさらに半分の125に、といった減り方をします。
この減り方をグラフにすると、下のようになります。
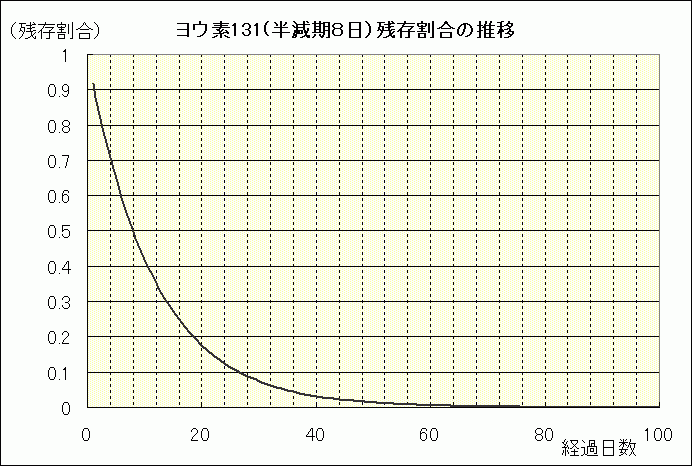
これを見ると、放射性崩壊して1ヶ月くらいすれば、存在するヨウ素131の量は10%程度にまで減少することがわかります。
■半減期から古美術品の製造時期が推定できる■
ここで、半減期をT日として、、崩壊が始まってから何日目には残存量がどのくらいになっているかを表す式を考えてみます。
崩壊が始まったときの量を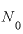 、経過日数を「t日」、t日目の残存量をNとすると、
、経過日数を「t日」、t日目の残存量をNとすると、
経過T日目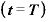 ……
…… 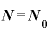 ・
・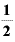
経過2T日目(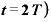 ……
…… 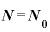 ・
・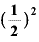
経過3T日目(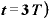 ……
…… 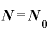 ・
・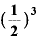
このように、経過日数tが「1×T」日目ならば、残存量は「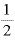 の1乗」、tが「2×T」日目なら残存量は「
の1乗」、tが「2×T」日目なら残存量は「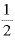 の2乗」、tが「3×T」日目なら残存量は「
の2乗」、tが「3×T」日目なら残存量は「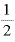 の3乗」という形になります。
の3乗」という形になります。
この関係をよくよく見ると、「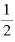 を何乗するか」の値は「
を何乗するか」の値は「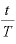 」と同じです。
」と同じです。
つまり、t日経過したときの残存量Nは、
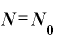 ・
・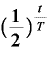 ……(A)
……(A)
という式で表すことができるわけです。
この式を使う例としてよく登場するのは、発掘された化石や古美術品などがいつ頃のものかを推定する年代測定です。
その測定には、安定している元素である炭素12と、その放射性同位体炭素14が用いられます。
大気中の炭素(気体)には炭素12と炭素14が一定の割合で存在しています。そうすると、たとえば、それを取り込んでいる植物も炭素12と炭素14がある割合で含まれていることになります。
ただし、その植物が生命を絶たれると、炭素14は放射性崩壊によって数が減っていきます。一方、炭素12のほうは崩壊しませんから、量は減りません。
その結果、その植物が摘まれたり、刈り取られたりすると、炭素12に対する炭素14の割合はどんどん減少していきます。
このことを利用すると、たとえば木製の工芸品や美術品、発掘品などの中に含まれている炭素12と炭素14の量の割合を調べることによって、材料の木材が何年前に伐採されたものかを推定することができてしまいます。
ある木製のテーブルの炭素12の量と炭素14の量を測定したところ、材料となっている木が生育しているときの一定割合の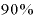 になっていたとしましょう。
になっていたとしましょう。
生育していたときの炭素12に対する炭素14の割合をkとすると、
(生育時) 炭素12の量:炭素14の量=1:k
 生育時の炭素14の量
生育時の炭素14の量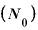 =炭素12の量×k
=炭素12の量×k
(テーブル) 炭素12の量:炭素14の量=1: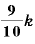
 いまの炭素14の量(
いまの炭素14の量(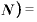 炭素12の量×
炭素12の量×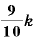
つまり、生育時の炭素14の量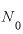 とテーブルの炭素14の量
とテーブルの炭素14の量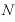 は
は

という関係です。
炭素14の半減期は約5600年です。この木材が伐採されてからの経過年数をtとして、先ほどの(A)式に当てはめると、
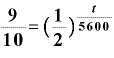
という式ができます。
この式を対数に変換すれば、経過年数tが出てきます。
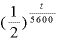 は書き換えれば「
は書き換えれば「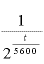 」になるので、
」になるので、
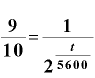
両辺逆数にして
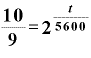
これを対数の形にします。そうすると、
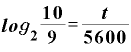
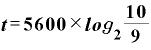
で、経過年数は「5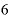 00×
00×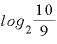 」年です。
」年です。
これが具体的に何年なのかは、「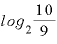 」の値を計算すればわかります。
」の値を計算すればわかります。
Excelで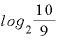 を計算してみると、その値は
を計算してみると、その値は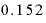 。これを入れれば
。これを入れれば
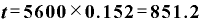 (年)
(年)
このテーブルは、850年前に伐採された木材で作られたと推定されるわけです。
もっとも、その木材が伐採されてすぐにテーブルが作られたかどうかはわかりませんが、もし古美術商が「1500年前に作られたものだ」と言ったら、それはちょっと胡散臭い、ということになります。
■半減期自体はどうやって求めるのか■
この木材が伐採された年代を推定する式は、予め半減期が分かっているので答えが出せます。
では、ある物質の半減期そのものを計算するにはどうすればいいのでしょうか。
一般的には、半減期を求める式も、また、先ほどの年代推定などの式も、微分や積分を使うのですが、ここでは、微分積分なしで考えてみます。
まず、前に出てきた(A)式を変形して、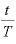 を表す対数にします。
を表す対数にします。
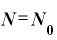 ・
・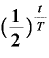
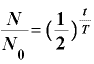
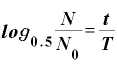
そうすると、半減期Tは、
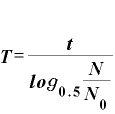
という式で表されます。
この値がいくらになるかは、その物質の具体的なデータが必要です。
たとえば「この物質の原子核の数は10年間でもとの数の99.876%になった」という測定データがすでにあるとします
つまり、経過した年数tは「10年」、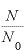 が「0.99876」です。
が「0.99876」です。
このデータを式に入れると、
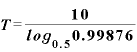
面倒そうな式ですが、対数部分の「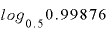 」はExcelなどを使えばすぐに値が出てきますから、単なる分数と考えて差し支えありません。
」はExcelなどを使えばすぐに値が出てきますから、単なる分数と考えて差し支えありません。
対数部分を計算すると、その値は0.00179。この値を入れれば、
半減期T=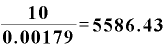 (年)
(年)
約5600年と出てきます。
ちなみに、この物質が炭素14です。 ◇