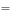 2.71828…」という値■
2.71828…」という値■年複利回数が大きくなると残高が”定額”に近づく理由とは
■自然科学になくてはならない「e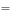 2.71828…」という値■
2.71828…」という値■
本書の中で何度か述べているように、複利の効果は非常に大きいものがあります。
そして、残高の増え方は、年1回複利よりも年2回複利のほうが、年2回複利よりも年4回複利のほうが大きくなります。
つまり、年複利回数が多いほうが、「より有利に増やせる」わけですが、複利回数が多くなればなるほど残高はどんどん増えていくのか、というと、実はそうではありません。
年間の複利回数が大きな数字になると、年間の元利合計額は”定額”化してしまうのです。
これは一体なぜでしょうか。
まず、改めて複利計算の式を見てみましょう。
金利をr、期間をT年とすると、年1回複利の元利合計額は、
元本×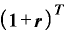
で表されます。元利合計額は当初元本の「(1+r)のT乗」倍になる、ということなので、以下では「元本×」の部分は省略します。
年2回複利の場合は、
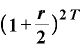
と、1回の利払い時にもらえる金利分は2分の1に減るものの、指数部分が「2T乗」と大きくなります。
年m回複利ならば、
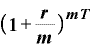
です。
複利回数mの値が非常に大きな数になると、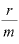 の値は限りなくゼロに近づき、
の値は限りなくゼロに近づき、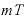 乗の値はとてつもなく大きな数になります。
乗の値はとてつもなく大きな数になります。
そういう状況になると、何かが起きるのでしょうか。
ここで、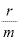 をhという文字に置き換えてみます。すなわち、
をhという文字に置き換えてみます。すなわち、
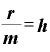
とします。
そうすると、mという文字は、
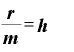
 →
→ 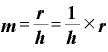
という形で表現できます。
この表現を使って「年m回複利」の式を書き換えると、
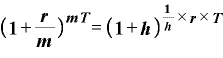
という式に変わります。
前のリンク部分「0.5乗とはどういう意味なのか」のところに登場した「指数法則その5」を使えば、この式は
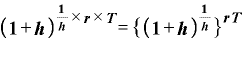
という書き方にできます。
この式を言葉で表現するならば、「1にhを足したものを、h分の1乗する。それをさらに『r×T』乗する」となります。
ここで{}内の「1にhを足したものを、h分の1乗する」というところに注目します。
実は、この「1にhを足したものを、h分の1乗する」という式、hの値を限りなくゼロに近づけると、”ある一定の数”に収束することが、偉大なる先人たちの研究でわかっているのです。
その”ある一定の数”はネイピア数と呼ばれ、「e」という文字で表現されます。
”一定の数”とは、
ネイピア数e=2.7182818…
という値で、小数点以下は循環することなく延々と続きます。(円周率πのような値、無理数です)
先述したように、mの値が大きくなると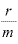 の値はどんどん小さくなり、mが非常に大きくなれば
の値はどんどん小さくなり、mが非常に大きくなれば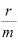 (=h)はほとんどゼロといってもいいような極々小さい数になります。
(=h)はほとんどゼロといってもいいような極々小さい数になります。
高校でやった「極限」の書き方を使うと、
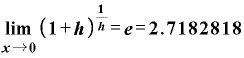 …
…
です。
ちなみに、hを限りなくゼロに近づけるということは、「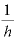 を限りなく∞に近づける」ということでもあります。
を限りなく∞に近づける」ということでもあります。
そうすると、たとえばhを「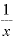 」に、「
」に、「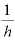 」を「x」に置き換えた場合には、この式は、
」を「x」に置き換えた場合には、この式は、
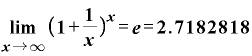 …
…
という表し方もできます。
どちらも同じ意味で、これがネイピア数の定義式とされます。(このeという数やその定義は高校の数Ⅲで出てきます)
この数の最も古い研究の発表はジョン・ネイピアという学者が行ったとされ、それゆえ「ネイピア数」と呼ばれているのですが、もともとはヤコブ・ベルヌーイという大数学者がこの形の式を立て、その具体的な数値を求めようとしたものとも言われます。
この式の値を「e」という文字(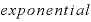 (指数関数)の頭文字)で表現したのがレオンハルト・オイラーという、これまた偉大な大数学者でした。
(指数関数)の頭文字)で表現したのがレオンハルト・オイラーという、これまた偉大な大数学者でした。
この「e」は、非常に不思議で便利な値で、たとえば、これを底とした指数関数「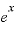 」は微分しても積分しても「
」は微分しても積分しても「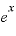 」になるという性質を持っています。
」になるという性質を持っています。
また、eを底とした対数(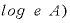 は自然対数と呼ばれ、物理学をはじめとする自然科学分野では非常に頻繁に使われます。具体的なところはまた改めて紹介しますが、自然科学分野になくてはならないもの、といっても全く過言ではない数値なのです。
は自然対数と呼ばれ、物理学をはじめとする自然科学分野では非常に頻繁に使われます。具体的なところはまた改めて紹介しますが、自然科学分野になくてはならないもの、といっても全く過言ではない数値なのです。
経済学の分野でも、たとえば統計学関連にeがよく出てきます。金融分野もしかりです。
この「e」という数値を用いると、年複利回数mが非常に大きい数字になったときの元利合計額は
元利合計額=元本×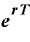
という式で表現できます。
「e」は”一定の数”ですから、rとTが同じであれば、元利合計額は”定額”になるわけです。
元本を100として、金利rが4%、期間Tが30年とすれば、
元利合計額=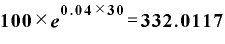
と、本文中で紹介している数字になります。
T=1、すなわち1年後の元利合計額は、
元本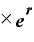
で表されます。
この「eのr乗」とは何なのかというと、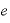 の定義が
の定義が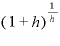 (の極限)で表されることと、
(の極限)で表されることと、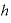 が「
が「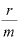 」を置き換えた文字であったことを思い出すと、
」を置き換えた文字であったことを思い出すと、
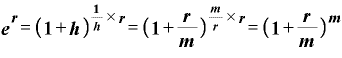
となって、「年複利回数がmの複利計算式でT=1のとき」の値と一致することがわかります。
m=1、すなわち年1回複利であれば、「eのr乗」は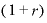 です。
です。
■「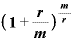 」なる式は一体何を表しているのか■
」なる式は一体何を表しているのか■
eの値を求める式「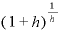 」は、もともとはヤコブ・ベルヌーイという大数学者が立てたもの、と述べましたが、一体何のためにこんな式を考えたのかというと、それは利子の複利計算式との関連だったいう説があります。
」は、もともとはヤコブ・ベルヌーイという大数学者が立てたもの、と述べましたが、一体何のためにこんな式を考えたのかというと、それは利子の複利計算式との関連だったいう説があります。
自然科学分野になくてはならない値の根源が実は「複利計算」にあったとすれば、これは非常に興味深いことではないでしょうか。
それにしても、このeという数値、その定義「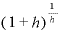 」という式、あるいは、
」という式、あるいは、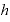 を「
を「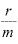 」に戻したときの
」に戻したときの
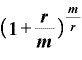
なる式は、一体何を表しているのでしょうか。
この式の中の「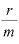 」は、「年利rを複利回数mで割った値」ですから、1回あたりの利子率を意味することはわかります。
」は、「年利rを複利回数mで割った値」ですから、1回あたりの利子率を意味することはわかります。
では、その逆数、指数の部分「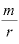 」は、どういう意味なのでしょうか。
」は、どういう意味なのでしょうか。
ここで、今さらながらですが、分数というものについて考えてみます。
たとえば、樽の中にある1.8リットルの日本酒を柄杓で10回、同じ量ずつ掬って樽を空にするとします。
そうすると、1回に掬う量は「1.8リットル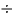 10回」で
10回」で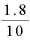 リットル。1.8リットルを回数10で割ることによって、「単位回数当たりに掬う量」が得られます。
リットル。1.8リットルを回数10で割ることによって、「単位回数当たりに掬う量」が得られます。
この計算は、年利rを年複利回数mで割った「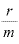 」が「単位利払い回数当たりの利子率」のような感じです。
」が「単位利払い回数当たりの利子率」のような感じです。
これを「10回÷1.8リットル」の「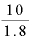 」としたら、どんな意味になるでしょうか。
」としたら、どんな意味になるでしょうか。
これは、「単位リットル当たりの掬い回数」、というと言い方がちょっと変ですが、つまり、1リットルという単位量が汲み上げられるのは、柄杓何回分に相当するか、を示します。「柄杓で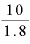 回(杯)汲み上げた量が1リットル」というわけです。
回(杯)汲み上げた量が1リットル」というわけです。
同じように考えると、「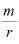 」は、「『単位当たりの金利』になるのは、利子をもらう回数にして何回に相当するか」を示します。要するに、「何回利子をもらうと、『単位当たりの金利』になるか」です。
」は、「『単位当たりの金利』になるのは、利子をもらう回数にして何回に相当するか」を示します。要するに、「何回利子をもらうと、『単位当たりの金利』になるか」です。
この「単位当たりの金利」とは何でしょうか。
金利は4%とか5%だから、「単位当たりの金利」は1%か、というとそうではありません。
金利rは0.04なり0.05なりという数字を用いて計算していますから、1%は0.01という数値になります。0.01は「単位」とは言いません。
「単位当たり」という場合の「単位」とは1です。「1」ということは、金利%で言うならば「100%」です。
つまり、「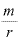 」は、「何回利子をもらうと、金利100%になるか」を表していることになります。
」は、「何回利子をもらうと、金利100%になるか」を表していることになります。
金利100%とは何かというと、単利で考えたときに「金利でもらう額が元本額と同じになる」ことを意味します。
それに必要な利子をもらう回数が「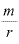 回」であり、「
回」であり、「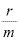 」の利率分を「
」の利率分を「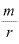 」回もらうと、単利では元本が2倍になる、ということです。
」回もらうと、単利では元本が2倍になる、ということです。
単利の式では、年m回利払いがあった場合の元利合計は「元本×(1+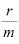 ・
・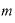 ・
・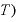 」となり、mが約分されて、結局は年1回利払いの式「元本×
」となり、mが約分されて、結局は年1回利払いの式「元本×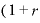 ・
・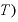 」と同じになります。
」と同じになります。
つまり、単利の場合の期間Tは、「年利r分をもらう回数」を示すものでもあるわけです。
では、年利rを何回もらうと「金利100%」、すなわち元本が2倍になるでしょうか。
答えは、「年利rの逆数回」です。
たとえば、年利rが4%(0.04=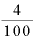 )であれば、その逆数の
)であれば、その逆数の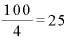 年分(25回分)の利払いをもらえば「年利r×回数」は1になります。
年分(25回分)の利払いをもらえば「年利r×回数」は1になります。
期間(=利子をもうら回数)Tを、年利rの逆数「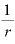 」として単利の式に当てはめれば
」として単利の式に当てはめれば
元本×(1+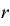 ・
・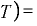 元本×(
元本×(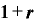 ・
・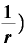 =元本×2
=元本×2
と、確かに元本は2倍になっています。
この「年利rのとき、単利で元本が2倍になる期間T=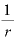 」を年1回複利で運用したら、元本はどのくらい増えるのでしょうか。
」を年1回複利で運用したら、元本はどのくらい増えるのでしょうか。
金利r、期間T=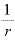 を年1回複利の式に入れてみると、、
を年1回複利の式に入れてみると、、
元本×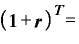 元本×
元本×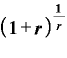
と、これはまさにeの定義の式「(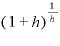 」と同じ形ではありませんか。
」と同じ形ではありませんか。
また、年複利回数m回の複利計算の式「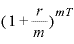 」の期間Tを
」の期間Tを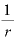 としてみると、
としてみると、
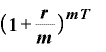 →
→ 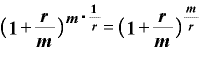
と、これは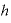 を「
を「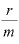 」に戻した式です。やはりeの定義式と同じになるのです。
」に戻した式です。やはりeの定義式と同じになるのです。
ということは、e=2.7182818…という数字は、「金利rのときに、単利で元本が2倍になる年数分を複利運用したとすると、元本は何倍になるか」を示していると解釈できます。
つまり、単利で元本が2倍になるのと同じ年数分(利子をもらう回数分)、同じ金利で複利運用すると、元本は「e」倍、すなわち、2.7182818…倍に収束する、というわけです。
最初に見たように、「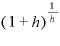 」で計算される値がe=2.7182818…に収束するのは「hが極めて小さい値、その逆数の
」で計算される値がe=2.7182818…に収束するのは「hが極めて小さい値、その逆数の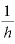 は非常に大きい値」という極限の場合ですが、よほどの高金利でない限りは、概ね「単利で元本が2倍になるとき、複利では元利合計は2.7倍程度になる」と考えてよいでしょう。
は非常に大きい値」という極限の場合ですが、よほどの高金利でない限りは、概ね「単利で元本が2倍になるとき、複利では元利合計は2.7倍程度になる」と考えてよいでしょう。
金利水準が低くても、期間が金利の逆数相当の長さであれば、単利でも元本は2倍になります。そのとき複利運用すれば、元本はより増えて2.7倍以上です。
超低金利下でも、元本を増やしていきたいなら、やはり「複利」に限る、と言って間違いありません。 ◇