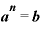 」という形の指数の式を逆から表現する、つまり、「
」という形の指数の式を逆から表現する、つまり、「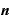 イコール」の形で表現するものです。
イコール」の形で表現するものです。logとは何を表現するものなのか
■指数関数を逆から表現したものが対数関数■
対数関数は指数関数とともに、高校の数ⅡBで出てきます。
当時のことを思い出すと、指数関数は「まぁ、それなりにわかる」という感じでしたが、対数については「???」だったような印象があります。
その理由は、第一には勉強しなかったからにほかなりませんが、たぶん「log」なる表記にどん引きした面もあるのではないかと思います。
logなるもの、対数とは何なのかというと、「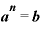 」という形の指数の式を逆から表現する、つまり、「
」という形の指数の式を逆から表現する、つまり、「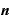 イコール」の形で表現するものです。
イコール」の形で表現するものです。
たとえば、「2を3回足すといくらになるか」は「2×3」という掛け算で表現します。これを「6は2を何回足したものか」という形にしたものが「6÷2」という割り算です。
この「3」に相当する値をx、「6」に相当する値をyとして一次関数で表現すれば、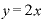 というを「xイコール」という形にすると「
というを「xイコール」という形にすると「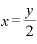 」になります。、
」になります。、
これと同じで、「2を3回掛けたらいくらになるか」を表現するのが「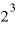 」、これを「8は2を何回掛けたものか」というふうに、逆から表現したものが「
」、これを「8は2を何回掛けたものか」というふうに、逆から表現したものが「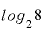 」という対数です。
」という対数です。
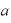 を
を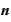 乗した値を
乗した値を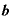 とすると、
とすると、
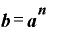 ⇔
⇔ 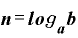
という関係です。
どちらもaを「底」、対数のbの値を「真数」と呼びます。
底aには「a>0 かつ a≠1」という条件があります。
というのは、底aが0では、何乗したところで0。a=1の場合も、何乗したところでbは1にしかなりません。
また、aがマイナスの場合には、累乗する指数部分が奇数のときにはbはマイナス、偶数のときにはプラスになる、といった具合に、bがプラスマイナス振動をして
しまいます。
対数の真数bには「b>0」という条件があります。底aが0より大きい数であれば、「aのn乗」の値bも0より大きい数になるからです。
なお、「n乗」のnには条件はありません。nは∞でも、マイナス∞でも、1でも0でもOKです。
ちなみに、nの値をマイナス∞にすると、bの値はほとんどゼロといってもいいくlらい小さな値になりますが、完璧ゼロにはならず、「b>0」は満たします。
■指数の値は「定率ずつ増えていく期間」と捉える■
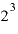 や
や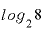 について「2を3回掛ける」「2を何回掛けたものか」などと表現しましたが、実際には、「掛ける回数」で考えると少々わかりにくくなることが出てきます。
について「2を3回掛ける」「2を何回掛けたものか」などと表現しましたが、実際には、「掛ける回数」で考えると少々わかりにくくなることが出てきます。
「0.5乗とは一体どういう意味か」でも出てきたように、「何乗」という指数の部分は小数点がついている数の場合もあれば、分数の場合も、負の数の場合もあります。
指数の部分を「掛ける回数」として考えると、0.5乗は「0.5回掛ける」、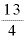 乗は「
乗は「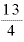 回掛ける」、マイナス5乗は「マイナス5回掛ける」ということになり、なんだか意味がわかりません。
回掛ける」、マイナス5乗は「マイナス5回掛ける」ということになり、なんだか意味がわかりません。
これを「回数」ではなく、たとえば秒なり、年数なりという、連続した期間(時間)だと考えると、途端にわかりやすくなります。
まさに複利の計算がそれですが、指数の部分を「定率ずつ複利的に増えていく年数」として考えれば、0.5乗は「半年後」、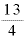 乗は「3年3ヶ月後」の状況、ということになります。
乗は「3年3ヶ月後」の状況、ということになります。
ではマイナス5乗は?
マイナスというのは「いまから遡って」と解釈することができますから、マイナス5乗は「いまから5年前」という過去の状況を表しているわけです。
そして、「定率ずつ」の部分が底になります。「2の何乗」という場合なら、「毎年2倍(200%)ずつ増えていく」、「1.04の何乗」という場合なら、「毎年1.04倍(4%)ずつ増えていく」という意味です。
もし、「最初100だったものが、毎年2倍ずつ複利的に増えていったとき、5年後にはいくらになっているか」というように、「最初にいくらある」というもとの数が特定されている場合には、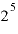 にもとの数を掛けます。。
にもとの数を掛けます。。
もとの数をk、底(増えていく率)をaとして、n年後の値をbとすれば、
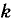 ・
・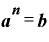
という式になります。
もとの数kが1であれば、bは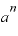 そのものの値です。
そのものの値です。
これをもとに対数を考えてみます。
たとえば、「毎年2倍ずつ複利的に増えていったとき、もとの数『1』がn年後に10になった」とします。
これを「2のn乗」の式で表すと、
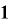 ・
・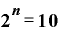
これを、「毎年2倍ずつ複利的に増えていったとき、もとの数『1』が10になる年数」という表現にしたものが、
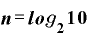
という対数です。
「最初100万円あったものが、毎年4%(1.04倍)ずつ複利で増えていったとき、130万円になるのはn年後」であれば、
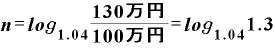
となります。
この対数の真数は1.3ですが、これは結局、「もとの数がn年後に1.3倍になっている」ことを示しています。
つまり、底がa,真数がbという対数は、「毎年a倍ずつ複利的に増えていった場合、もとの数がb倍になっているのは何年後か」を表しているわけです。
複利の計算でいえば、底は「1+金利r」、真数は「元利合計額が元本の何倍になっているか」で、その対数で表現されるのが複利運用する年数Tです。
かつて対数を習ったとき、「logなんていうもの、一体何に使うのか」と思った人もいるのではないでしょうか。その後文系に進んだ人だと、実際に何にも使わなかったかもしれませんが、お金の運用を考える中では、このlogなるものが役に立ちます。
高校のときにはわからなかった、学校で習う数学の実用例のひとつだと思います。
■対数関数のグラフは指数関数のグラフと対称の形■
指数関数と呼ばれる関数は、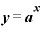 といった形で表されるのが一般的で、この式のaは定数
、xはいろいろな値をとる変数、yは「xを変えていったときの値」です。
といった形で表されるのが一般的で、この式のaは定数
、xはいろいろな値をとる変数、yは「xを変えていったときの値」です。
一方、対数関数は、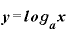 といった形で表現されます。aはやはり定数で、「真数部分の x の値を変えていったとき、yの値はどうなるか」という意味です。
といった形で表現されます。aはやはり定数で、「真数部分の x の値を変えていったとき、yの値はどうなるか」という意味です。
指数関数と対数関数、それぞれxの値を変えていくとyの値はどんな感じで変化していくのか。ここで、指数関数と対数関数のグラフを見ておきましょう。
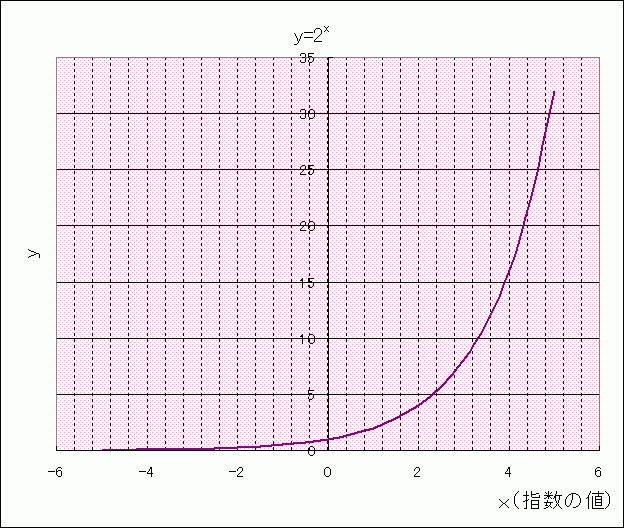
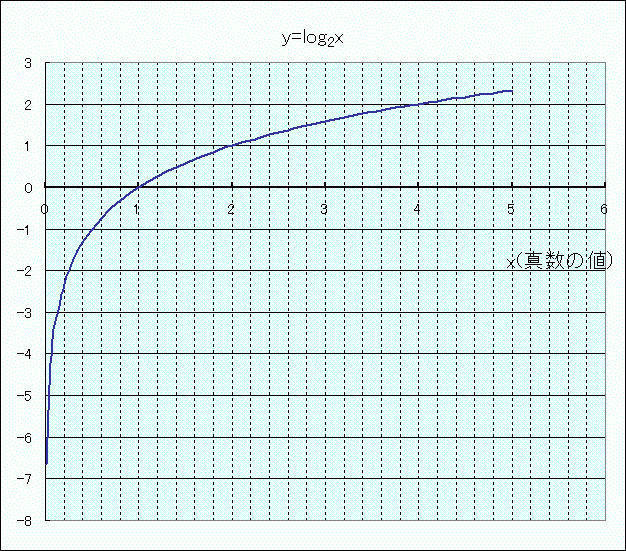
上のグラフは、a=2のときの指数関数と対数関数のグラフです。aの値が1より大きい場合、両者のグラフは「y=x」の直線に関して対称な形を描きます。
aの値が、0<a<1の場合は、下のような形になります。
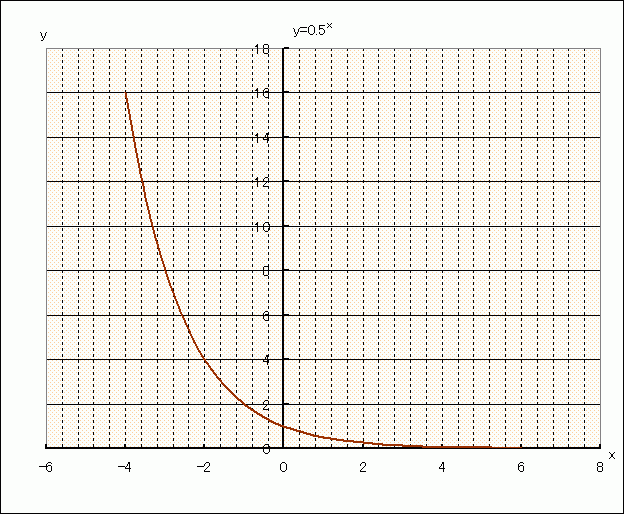
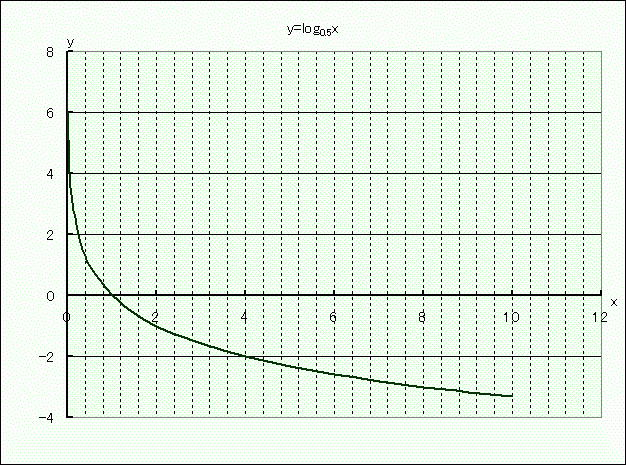
このグラフはa=0.5のケースです。 ◇