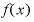 があったときに
があったときに微分すると「変化の様子」が見えてくる(1)
■微分の基本は、意外なほどに単純な割り算■
かつて数学が苦手だったという人にとって、微分と積分は「これは一体何のためのものなのか」と強く感じた、まさに最たるものではないでしょうか。
自分がまさにそうだったわけですが、まず、極限「lim」なるものが出てきて「??」。そのあと、「xの2乗を微分すると2xになる」というような機械的に覚えられるものは覚えたものの、その意味など全く分からず。一体どういうことをやっていたのか、記憶にすら残っていないのが実情だったりします。
ところが、試験や受験のプレッシャーがない状況のもとで考えてみると、微分というものの基本は、意外なほどに単純な作業であることに気付きます。
「微分する」というのは具体的に何をすることかというと、たとえば、「y=xをどうにかこうにかする」という関数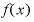 があったときに
があったときに
(「微分」という作業の手順)
①まず、1つxの値を決める。これをたとえば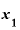 とする。
とする。
②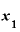 よりも極々わずかに大きいところにもう1点、
よりも極々わずかに大きいところにもう1点、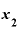 をとる。
をとる。
③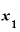 のときのyの値「
のときのyの値「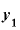 」と、
」と、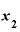 のときのyの値「
のときのyの値「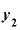 」を計算する。
」を計算する。
④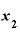 から
から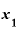 を引いて、その差を出す。
を引いて、その差を出す。
⑤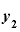 から
から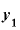 を引いて、その差も出す。
を引いて、その差も出す。
⑥「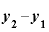 」を「
」を「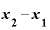 」で割る。
」で割る。
ということをします。
つまり、2つのxの差で2つのyの差を割る、という単純な割り算です。この割り算をすることが「関数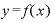 をxで微分する」ということです。
をxで微分する」ということです。
■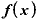 が「
が「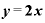 」という一次関数を微分してみる■
」という一次関数を微分してみる■
たとえば、関数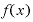 の中身が「xに2を掛ける」というものだとします。その結果をyという文字で表現するとすれば、
の中身が「xに2を掛ける」というものだとします。その結果をyという文字で表現するとすれば、
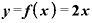
という表現になります。
たとえば、1年間に2万円の利払い金が出る債券があって、その利払い金を貯めていったとき、「x年後には残高はy万円増えている」というような状況は、この式で表されます。
まず、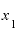 として「1」をとってみます。
として「1」をとってみます。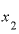 は、それより1だけ大きい「2」にします。
は、それより1だけ大きい「2」にします。
「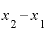 」は言うまでもなく「1」です。
」は言うまでもなく「1」です。
それぞれに対応するyの値は、
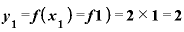
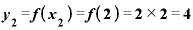
で、2つのyの差「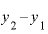 」は「2」です。
」は「2」です。
この2つのyの差「2」を、2つのxの差「1」で割ると、答えは2。
以上、これで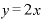 を微分する、という作業はおしまいです。
を微分する、という作業はおしまいです。
それはあまりにも単純すぎないか、という気がしないでもないかもしれません。
ここで、改めて「微分の作業の手順」を見てみると、「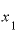 よりも極々わずかに大きいところに
よりも極々わずかに大きいところに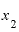 をとる」となっています。
をとる」となっています。
いま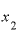 を2としたわけですが、これが
を2としたわけですが、これが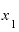 よりも極々わずかに大きい数なのか、というと、そうとは言えない可能性もあります。
よりも極々わずかに大きい数なのか、というと、そうとは言えない可能性もあります。
そこで、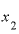 の値をもっと小さく、1.001としてみます。
の値をもっと小さく、1.001としてみます。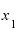 と
と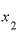 の差は「0.001」ですから、確かに極々わずかな感じがします。
の差は「0.001」ですから、確かに極々わずかな感じがします。
そうすると、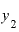 の値は、
の値は、
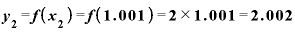
です。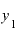 は先ほどと同じ2ですから、
は先ほどと同じ2ですから、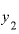 との差は0.002.
との差は0.002.
これを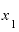 と
と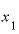 の差0.001で割ると、答えはさっきと同じ2.
の差0.001で割ると、答えはさっきと同じ2.
もっともっと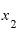 の値を
の値を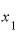 に近づけても、この割り算の答えは2にしかなりません。
に近づけても、この割り算の答えは2にしかなりません。
ならば、最初に決める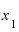 の値を「1」ではな「2」として、
の値を「1」ではな「2」として、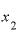 を「2.001」としてみたらどうでしょうか。2つのxの差は0.001です。
を「2.001」としてみたらどうでしょうか。2つのxの差は0.001です。
それぞれに対応する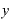 の値は、
の値は、
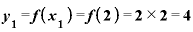
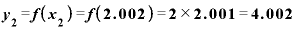
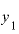 と
と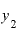 の差は0.002.これをxの差0.001で割ってみると、やっぱり今度も答えは2です。
の差は0.002.これをxの差0.001で割ってみると、やっぱり今度も答えは2です。
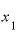 として他のどの値をとってみても、
として他のどの値をとってみても、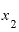 の値をもっともっと小さくしても、この割り算を計算すると、何をやっても答えは2にしかなりません。
の値をもっともっと小さくしても、この割り算を計算すると、何をやっても答えは2にしかなりません。
つまり、「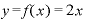 をxで微分すると2になる」ということなのです。
をxで微分すると2になる」ということなのです。
この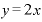 が「毎年2万円の利払い金を貯めていったとき、x年後までに残高が増えた額」を表す式だとすると、これをxで微分した結果出てくる「2」とは、「1年後なり、2年後なり、各経過年時点におけるの残高yの増え方のペース」を
意味します。
が「毎年2万円の利払い金を貯めていったとき、x年後までに残高が増えた額」を表す式だとすると、これをxで微分した結果出てくる「2」とは、「1年後なり、2年後なり、各経過年時点におけるの残高yの増え方のペース」を
意味します。
この場合、1年後時点でも、2年後時点でも、何年後時点でも、増え方のペース、言うなれば”年速”は「2(万円)/年」で一定、というわけです。
■関数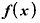 が「
が「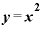 」という二次関数ならどうなるか■
」という二次関数ならどうなるか■
「毎年2万円ずつ利払い金をもらうのだから、残高が増えるペースは1年あたり2万円だ、というのは、当たり前すぎるじゃないか」と思ったかもしれません。
では、関数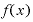 の中身が「xを2乗する」、すなわち
の中身が「xを2乗する」、すなわち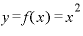 だったらどうなるでしょうか。
だったらどうなるでしょうか。
たとえば、最初の1年間では残高は1万円増え、次の1年間では4万円、その次の1年間では9万円増えていく、といった具合に、経過年数の2乗ずつ残高が増えていくようなイメージです。
まず、 を「1」、
を「1」、 を「1.1」としてみます。
その差は0.1です。
を「1.1」としてみます。
その差は0.1です。
それぞれに対応するyの値は、
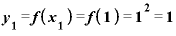
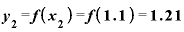
2つのyの差「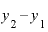 」は0.21です。
」は0.21です。
これをxの差「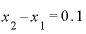 」で割ると、答えは2.1と出てきます。
」で割ると、答えは2.1と出てきます。
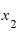 の値をもっと
の値をもっと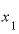 に近づけて、1.001とすると、
に近づけて、1.001とすると、
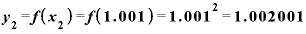
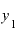 は1ですから、その差をxの差で割ると、
は1ですから、その差をxの差で割ると、
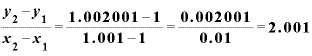
と、さっきの「2.1」とは違う答えが出てくるではありませんか。
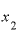 の値をもっともっと
の値をもっともっと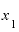 に近い1.0001にすると、
に近い1.0001にすると、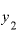 は、
は、
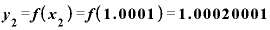
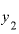 と
と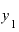 の差は0.00020001を、
の差は0.00020001を、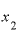 と
と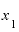 の差0.0001で割ると、答えは2.0001。
の差0.0001で割ると、答えは2.0001。
これまたさっきの答えとは違う値ですが、ここまでの3つの計算結果を比べてみると、いずれも「2+(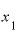 と
と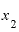 の差)」になっていることに気付かないでしょうか。
の差)」になっていることに気付かないでしょうか。
それゆえ、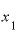 と
と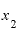 の差が小さくなると、小数点以下の値が小さくなり、そして、その値は2に近い値になってきています。
の差が小さくなると、小数点以下の値が小さくなり、そして、その値は2に近い値になってきています。
とすると、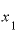 と
と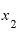 の差をほとんどゼロといっても差し支えないくらいに小さくしていったとしたら(ただし、完全にゼロにはしない)、おそらく、この割り算の答えは、「ほとんど2と言っても差し支えない値」になるに違いありません。
の差をほとんどゼロといっても差し支えないくらいに小さくしていったとしたら(ただし、完全にゼロにはしない)、おそらく、この割り算の答えは、「ほとんど2と言っても差し支えない値」になるに違いありません。
ということは、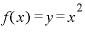 という関数を微分すると「2」になる、ということなのでしょうか。
という関数を微分すると「2」になる、ということなのでしょうか。
ここで、前にやったのと同じように、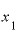 の値を変えて「2」としてみます。
の値を変えて「2」としてみます。
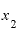 を2.001とした場合、2つのxの差は0.001.
を2.001とした場合、2つのxの差は0.001.
それぞれに対応する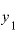 と
と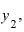 および、その差は、
および、その差は、
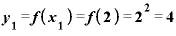
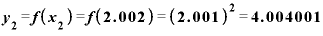
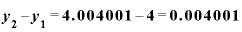
これをxの差0.001で割ると、答えは4.001。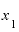 が「1」のときとは全く違う答えが出てきてしまいました。
が「1」のときとは全く違う答えが出てきてしまいました。
さらに、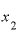 の値を2.0001としてみると、xの差は0.001、
の値を2.0001としてみると、xの差は0.001、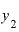 は
は
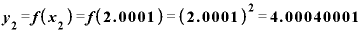
なので、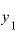 との差は0.004001.これをxの差0.001で割ると、答えは4.0001です。
との差は0.004001.これをxの差0.001で割ると、答えは4.0001です。
この2つの結果を比べてみると、今回は「4+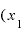 と
と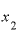 の差)」になっています。
の差)」になっています。
ということは、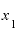 を2として、
を2として、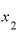 との差をほとんどゼロといっても差し支えなくくらい小さくしたら、この割り算の答えは「ほとんど4と言っても差し支えない値」になるのではないか、と考えられるところです。
との差をほとんどゼロといっても差し支えなくくらい小さくしたら、この割り算の答えは「ほとんど4と言っても差し支えない値」になるのではないか、と考えられるところです。
実際にやってみると、確かにそうなります。
■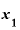 が「3」ならどうなるのか。「4」の場合は?■
が「3」ならどうなるのか。「4」の場合は?■
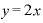 のときとは違って、
のときとは違って、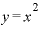 の場合には
の場合には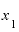 を「1」としたときと、
を「1」としたときと、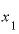 を「2」としたときとでは、割り算の結果が違うものになってしまいました。
を「2」としたときとでは、割り算の結果が違うものになってしまいました。
では、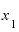 が「3」ならどうなるでしょうか。
が「3」ならどうなるでしょうか。
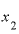 を3.0001とすると、
を3.0001とすると、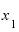 との差は0.001。
との差は0.001。
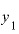 、
、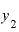 、およびその差は、
、およびその差は、
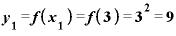
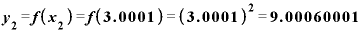
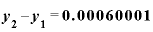
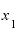 と
と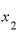 の差0.0001で
の差0.0001で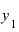 と
と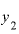 の差を割ると、答えは6.0001。
の差を割ると、答えは6.0001。
これまでの結果から予想するに、この割り算の結果は「6+(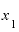 と
と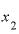 の差)」になりそうではないでしょうか。
の差)」になりそうではないでしょうか。
そして、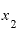 と
と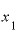 の差がほとんどゼロといっても差し支えないくらいに小さければ、この割り算の答えは「ほとんど6と言っても差し支えない値」になる、という予想もできそうです。
の差がほとんどゼロといっても差し支えないくらいに小さければ、この割り算の答えは「ほとんど6と言っても差し支えない値」になる、という予想もできそうです。
実際にやってみると、これまた確かにそうなります。
ここで、これまでの結果をまとめてみると、
◎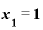 のとき、
のとき、 との差が極々わずかであれば、yの差をxの差で割った答えは「『2』といっても差し支えない値」になる
との差が極々わずかであれば、yの差をxの差で割った答えは「『2』といっても差し支えない値」になる
◎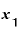 =
=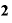 のときには、yの差をxの差で割った答えは「『4』と言っても差し支えない値」になる。
のときには、yの差をxの差で割った答えは「『4』と言っても差し支えない値」になる。
◎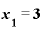 のときには、「『6』と言っても差し支えない値」になる。
のときには、「『6』と言っても差し支えない値」になる。
ということです。
この結果を見ると、「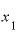 と
と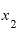 の差が極々わずかなとき、yの差をxの差で割った答えは、『
の差が極々わずかなとき、yの差をxの差で割った答えは、『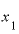 の2倍』といって差し支えない値」になっています。
の2倍』といって差し支えない値」になっています。
これが偶然でないとすれば、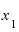 が「4」のときには、同じような割り算の答えは「8と言っても差し支えない値」になるはずです。
が「4」のときには、同じような割り算の答えは「8と言っても差し支えない値」になるはずです。
実際、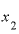 を4.0001としてみると、
を4.0001としてみると、
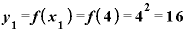
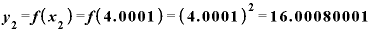
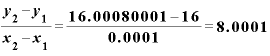
と、やっぱりそうです。
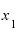 をほかのどんな値にしても、やはりyの差をxの差で割った答えは「『
をほかのどんな値にしても、やはりyの差をxの差で割った答えは「『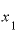 の2倍』と言って差し支えない値」になります。
の2倍』と言って差し支えない値」になります。
これこそが、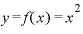 という関数をxで微分する、という作業で得られる結果です。
という関数をxで微分する、という作業で得られる結果です。