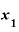 の2倍」という値は何を表しているのか■
の2倍」という値は何を表しているのか■微分すると「変化の様子」が見えてくる(2)
■「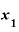 の2倍」という値は何を表しているのか■
の2倍」という値は何を表しているのか■
ところで、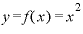 という関数をxで微分すると「
という関数をxで微分すると「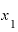 の2倍」になるという、この「
の2倍」になるという、この「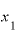 の2倍」とは一体何なのでしょうか。
の2倍」とは一体何なのでしょうか。
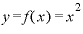 のグラフを見ながら考えてみます。
のグラフを見ながら考えてみます。
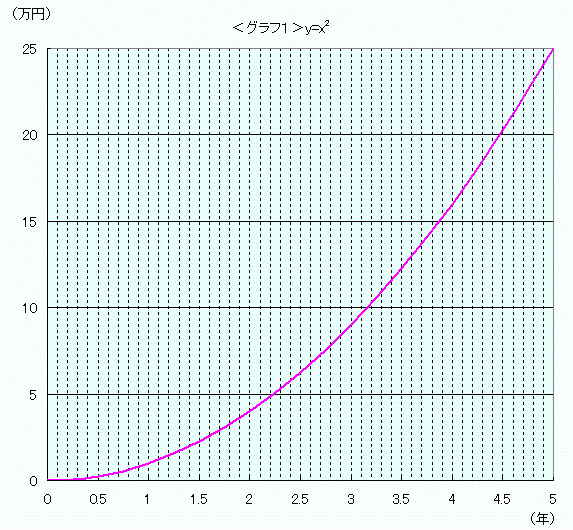
実際にはあり得ませんが、取りあえず、このグラフは「残高yが時間xの経過とともに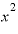 で増えていく魔法の預金」の様子を表していると思ってください。
で増えていく魔法の預金」の様子を表していると思ってください。
たとえば、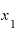 を2(年後時点)、
を2(年後時点)、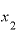 を4(年後時点)とします。残高は2年後時点で4万円、4年後時点で16万円ですから、2年間で12万円増えています。
を4(年後時点)とします。残高は2年後時点で4万円、4年後時点で16万円ですから、2年間で12万円増えています。
この増え方を「1年あたりどのくらいのペースで増えたか」、言わば”増え方の年速”で表現するとどうなるでしょうか。
2年で12万円ですから、「12万円÷2年」で6(万円/年)」。
と、言ってしまってよいものでしょうか。
2年後時点の残高4万円は、3年後時点では9万円と、5万円しか増えていません。その9万円が、その次の1年間で7万円増えた結果、3年後時点で残高は16万円になっているわけです。
そうすると、「12万円÷2年」という計算で出てきた6(万円/年)は、「2年後時点から4年後時点における、増え方の”平均年速”」と言わなければなりません。
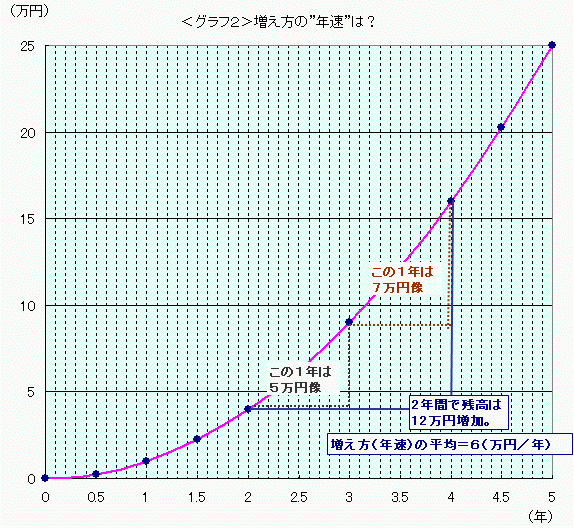
では、平均ではなくて、「ジャスト2年後時点における瞬間の増え方速度」はいくらなのでしょうか。
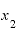 を3(年後時点)とすると、2年後から3年後までの1年間で5万円増えています。ならば、瞬間の増え方速度は「5(万円/年)」か、というと、これも「ジャスト2年後時点の瞬間増え方速度」とは言えません。
を3(年後時点)とすると、2年後から3年後までの1年間で5万円増えています。ならば、瞬間の増え方速度は「5(万円/年)」か、というと、これも「ジャスト2年後時点の瞬間増え方速度」とは言えません。
というのも、2年後時点から半年で2万2500円増え、2年半後時点からその後の半年間で2万7500円増えた結果、3年後時点で9万円になっているのですから、やはりこの「5(万円/年)」も平均の年速です。
結局、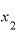 を
を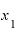 の2(年後時点)に近づけていっても、その間に時間差がある以上、その2時点から計算される増え方の速度は平均年速にしかなりません。
の2(年後時点)に近づけていっても、その間に時間差がある以上、その2時点から計算される増え方の速度は平均年速にしかなりません。
つまり、”ジャスト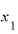 年後時点”の増え方速度を正確に知ることはできない、ということです。
年後時点”の増え方速度を正確に知ることはできない、ということです。
ただ、「正確に」ではありませんが、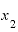 が
が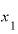 の2(年後時点)に極めて近い、その差をほとんどゼロといっても差し支えないくらいわずかなものすれば、、”ジャスト
の2(年後時点)に極めて近い、その差をほとんどゼロといっても差し支えないくらいわずかなものすれば、、”ジャスト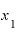 年後時点”の瞬間増え方速度といっても差し支えないような年速を出すことは可能ではないでしょうか。
年後時点”の瞬間増え方速度といっても差し支えないような年速を出すことは可能ではないでしょうか。
これがまさに微分です。
つまり、実際には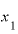 と
と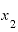 の2つの時点を考えてはいるものの、ほとんど1点にしか見えないくらいに双方を近づけることによって、それを”瞬間”として捉え、その瞬間の変化の様子を「単位あたりの変化(この場合は、年換算の増え方速度)」の形で表現するわけです。
の2つの時点を考えてはいるものの、ほとんど1点にしか見えないくらいに双方を近づけることによって、それを”瞬間”として捉え、その瞬間の変化の様子を「単位あたりの変化(この場合は、年換算の増え方速度)」の形で表現するわけです。
これをグラフ上で表すと、あたかも”ジャスト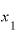 年時点”の1点で接する接線のように見えます。
年時点”の1点で接する接線のように見えます。
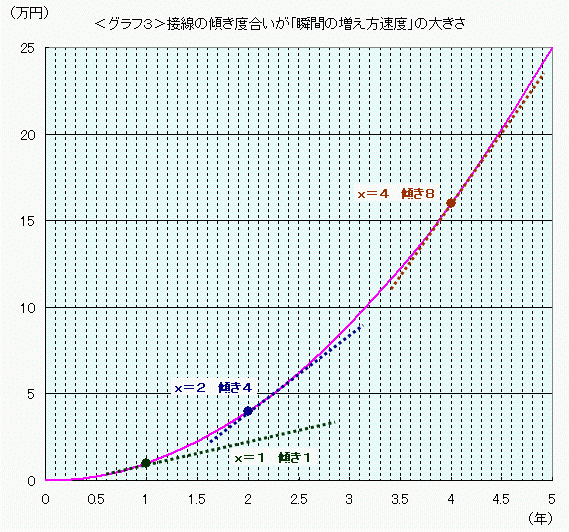
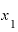 の値が大きくなればなるほど、接線の傾き度合いが急になっています。これは、
の値が大きくなればなるほど、接線の傾き度合いが急になっています。これは、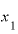 が大きくなるほど、増え方の年速が増している、加速していることを示します。
が大きくなるほど、増え方の年速が増している、加速していることを示します。
「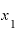 の2倍」とは、この接線(的なもの)の傾きを示す値です。つまり、「
の2倍」とは、この接線(的なもの)の傾きを示す値です。つまり、「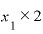 」の値は、
」の値は、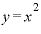 という関数で表される量の、各
という関数で表される量の、各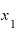 点における変化の速度、変化の様子を表している、ということです。
点における変化の速度、変化の様子を表している、ということです。
この「各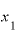 点における変化の様子」を表す式、
点における変化の様子」を表す式、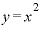 であれば「
であれば「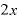 」は、導関数と呼ばれます。「微分する」というのは、この導関数を求める作業のことを指します。
」は、導関数と呼ばれます。「微分する」というのは、この導関数を求める作業のことを指します。
この「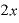 」という導関数のxの部分に、1なり、2なりという具体的な
」という導関数のxの部分に、1なり、2なりという具体的な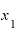 の数字を入れると、各
の数字を入れると、各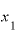 点における瞬間速度的な値が出てきます。この値は、その
点における瞬間速度的な値が出てきます。この値は、その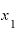 を接点とする接線の傾きでもあります。
を接点とする接線の傾きでもあります。
この瞬間速度的な具体的な値は微分係数と呼ばれます。
■微分の表現方法のいろいろ■
前ページでは、微分の手順として、差がわずかしかない2つのxの差「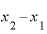 」で、それぞれのxに対応するyの差「
」で、それぞれのxに対応するyの差「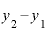 」を割る、という表現をしましたが、ここで、少し表現方法を変えてみます。
」を割る、という表現をしましたが、ここで、少し表現方法を変えてみます。
まず、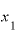 と
と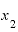 の差を「Δx」、
の差を「Δx」、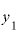 と
と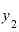 の差を「Δy」とします。すなわち、
の差を「Δy」とします。すなわち、

です。
そうすると、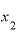 は「
は「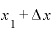 」という形で表すことができますから、
」という形で表すことができますから、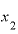 という文字はもう使う必要がなくなります。
という文字はもう使う必要がなくなります。
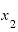 という文字を使わなくてもよいとなれば、
という文字を使わなくてもよいとなれば、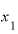 にも添え字をつけることはないでしょう。単に「x」としてしまいます。
にも添え字をつけることはないでしょう。単に「x」としてしまいます。
また、前のページで、「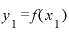 」
」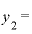 「
「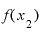 」などとしてきましたが、「
」などとしてきましたが、「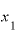 」を単にxにして、さらに「Δx」「Δy」という表現を導入すると、
」を単にxにして、さらに「Δx」「Δy」という表現を導入すると、
(旧)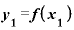 → (新)
→ (新)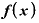
(旧)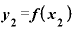 → (新)
→ (新)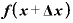
(旧)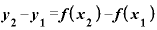 →
(新)
→
(新)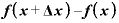
という書き方ができます。
さらに、「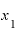 と
と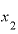 の差は極々わずかでしかない」ということは、「Δxが限りなくゼロに近い」と言い換えてもよいでしょう。
の差は極々わずかでしかない」ということは、「Δxが限りなくゼロに近い」と言い換えてもよいでしょう。
この「限りなく」感を「linit」を省略した「lim」という文字で表すことにします。
これらを使って、微分という作業を表現すると、
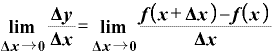
という形になります。
これが微分の定義で、これをせっせと計算して出てくる結果が導関数です。
「y=xをどうにかこうにかする」という関数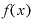 をxで微分する場合、いちいち「lim」と書くのも面倒なので、「ごくごく小さいΔx」「それに対応するΔy」をそれぞれ「dx」「dy」として、
をxで微分する場合、いちいち「lim」と書くのも面倒なので、「ごくごく小さいΔx」「それに対応するΔy」をそれぞれ「dx」「dy」として、
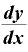
と書いたり、あるいは、
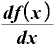
書いたりします。
さらに、もっと簡単に、「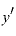 」や「
」や「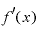 」のように、「’」をつけるだけで表現することもあります。
」のように、「’」をつけるだけで表現することもあります。
なお、ここでは「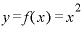 という関数を『xで』微分する」という言い方をしていますが、微分する場合には、「何で」微分するかが非常に大切です。
という関数を『xで』微分する」という言い方をしていますが、微分する場合には、「何で」微分するかが非常に大切です。
この「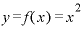 」という関数を「xで」微分するのは、「xが極々わずかに動いたときに、yの値の変化はどんな具合になるか」を調べるためです。
」という関数を「xで」微分するのは、「xが極々わずかに動いたときに、yの値の変化はどんな具合になるか」を調べるためです。
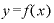 で表される関数のxに該当するものは独立変数、xの値がどうなるかによって決まるyに該当する値は、従属変数と呼ばれます。
で表される関数のxに該当するものは独立変数、xの値がどうなるかによって決まるyに該当する値は、従属変数と呼ばれます。
ちなみに、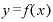 という関数を、xにもyにも全く関係ない独立した量(変数)、たとえば「z」で微分しても、「zが極々わずかに変化したとき、xおよびyは何も変化しない」となりますから、得られる結果(導関数)は「0」です。
という関数を、xにもyにも全く関係ない独立した量(変数)、たとえば「z」で微分しても、「zが極々わずかに変化したとき、xおよびyは何も変化しない」となりますから、得られる結果(導関数)は「0」です。
また、数学ではxやyという文字がよく使われますが、使う文字自体は何でもかまいません。
たとえば、「元利合計額Gは、年数tによってこういうふうに変化する」という関数であれば、
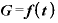
といった書き方になります。
この関数を「tで微分する」という場合は、
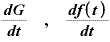
などと表現します。
「債券価格Pは、(1+金利)である『R』によって決まる値だ」という場合なら、その関数は、
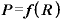
といった表現になり、「Rが極々わずかに変化したとき、債券価格Pの変化はどんな具合になるか」を調べる、すなわち「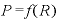 をRで微分する」作業は
をRで微分する」作業は
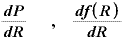
といった形で表現されます。 ◇