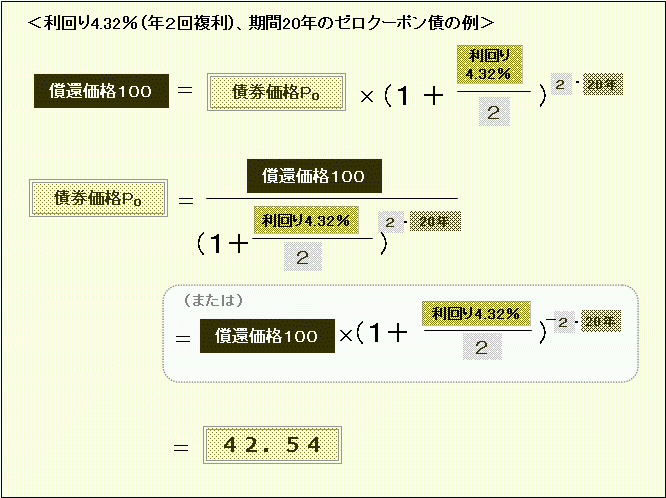
（１）割引債の利回りはなぜ複利で計算するのか
債券の利回りは、利付債の場合には単利換算の表示であったり、複利換算の表示であったり、国や地域の慣習などによって異なりますが、クーポンのない割引債（ゼロクーポン債）は、複利換算で表示されるのが一般的です。
米国のゼロクーポン債は、年２回複利換算の利回り表示となっています。
たとえば、2011年６月７日時点で期間20年のゼロクーポン国債の利回りは約4.32％。債券価格は42.54と計算されます。
この債券は、「42.54が20年後に１００になる」というものですから、これを単利換算すると6.75％という高さになります。
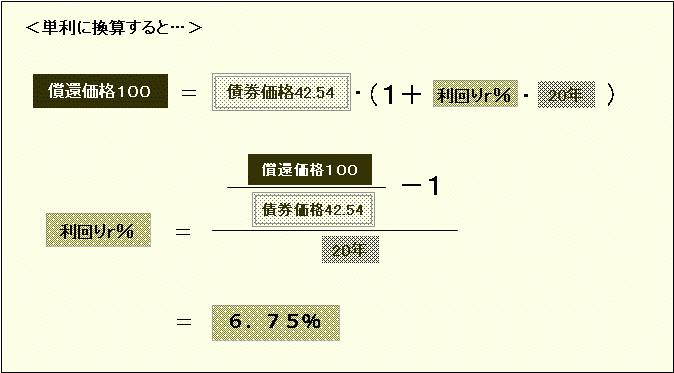
単利のほうがわかりやすいともいえるのですが、ただ、単利で考えると、計算上、元本の増え方が毎年下がっていくという、少々奇妙なことが生じてしまいます。
単利で6.75％というのは、「毎年、『42.54×6.75％＝2.87145』ずつ元本が増えていく」ことを意味すます。１年後には当初の42.54が2.87145増えて45.41145になり、２年後にはこれが2.87145増えて48.2829になり…、といった具合です。
そうすると、当初元本に対する１年後の利回りは6.75％ですが、1年後から２年後までの年利を計算すると「2.87145÷45.41145」の6.365％と、下がってしまいます。2年後から３年後までの年利はさらに下がって5.947％。19年後から20年後までの最後の１年間に至っては、年利2.956％になる計算です。
あくまでも計算上のことではありますが、これはちょっと「元本が成長していって償還時に１００になる」というゼロクーポン債の本質的な姿とは違うような気がしないでもありません。
これに対して、複利換算は「一定期間ごとに定率ずつ増えていく」と捉えまず。当初42.54の元本は半年後に年利回り4.32％の半分の2.16％増えて43.46になり、そのまた半年後にはそれよりも2.16％増えて44.40になり…、19年６ヶ月後から償還の20年後は97.893がやはり2.16％増えて１００になります。
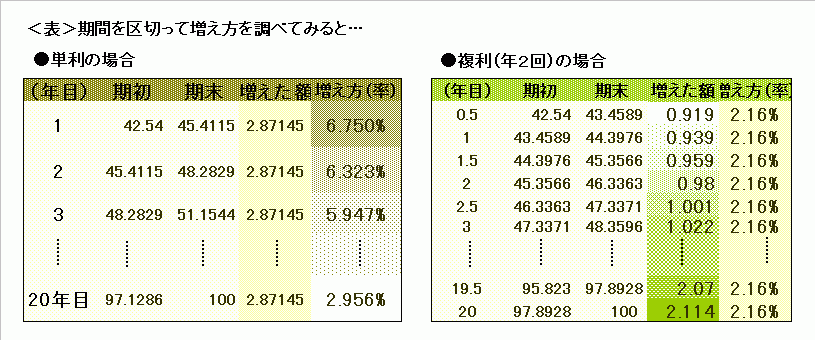
複利のほうが、確かにそれっぽい感じがするのではないでしょうか。
次は、（２）「毎日複利」の利回りは何％になるのか、です。
