(2)「毎日複利」の利回りは何%になるのか
もっとも、複利を適用する6ヶ月間を考えてみると、年2回複利でも「その時々で元本の増える率が違ってくる」ということが生じます。
たとえば、年2回複利の場合、スタートから3ヶ月後の元利合計額は42.997で、最初の42.54から0.457増えています。元本に対する増え方の率は1.074%です。
6ヶ月後には元利合計額は43.459ですから、3ヶ月後から6ヶ月後までの3ヶ月間の増加分は0.461。3ヶ月目の元利合計額に対する増え方の率は1.072%と、当初3ヶ月よりも低くなっています。
複利回数をもっと増やして、たとえば3ヶ月ごとの年4回複利で考えたとしても、1ヶ月後までと、1ヶ月目から2ヶ月目まで、2ヶ月目から3ヶ月目までで、それぞれ元本の増える率には差が出てきてしまうのです。
であれば、この際、毎日毎日複利で元本が増えていく、と考えてみてはどうでしょうか。それならば、「償還までのどの期間を切り取っても、いつでも定率ずつなめらかに元本が増え続けている」という姿を表すことができるはずです。
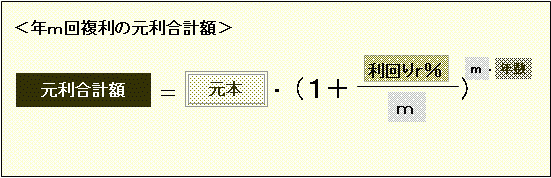
毎日複利で増えるということは、年複利回数が365回ということになります。年複利回数がm回の場合、元利合計額の計算式は

となりますが、「年複利回数が大きくなると残高はどのくらい増えるのか(2)」でも紹介したように、この「m回」が非常に大きい場合、だいたい100を超えるくらいになると、もはやmが増えていっても年間の元利合計額の増え方はほとんど変わらなくなります。年利回りをrとすると、1年間の増え方は「2.7182818のr乗」という“定額”に近い値になってしまうのです。(「なぜ?」という方は、こちら。 )
そうすると、年複利回数が大きい場合、T年後の元利合計額は「当初の元本×『2.7182818のrT乗』」という計算式で表される値になります。
この「2.7182818」は「e」という文字で表されるネイピア数と呼ばれる無理数です。このeという文字を使って、年複利回数が非常に大きい場合の元利合計額を表現すると、
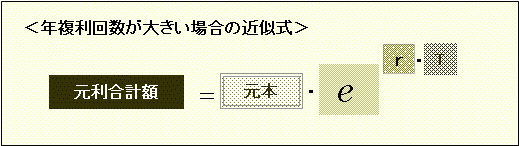
という形になります。
当初元本を42.54、期間20年、元利合計額を100とすれば、
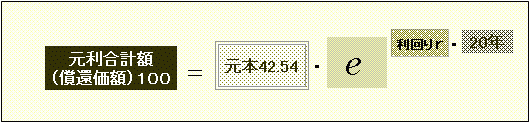
です。
では、この年利回りrは一体何%になるのでしょうか。
先の式を変形すると、
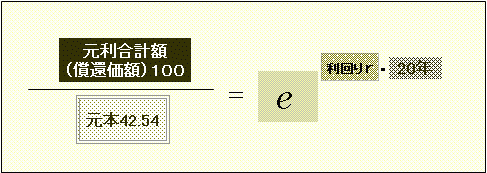
になります。
これは「『e』なる値を『20年×r』乗すると、『100÷42.54(=2.351)』になる」という意味ですから、指数の「r×20年」乗の部分は、「e」なる値を底とする対数によって表現することができます。(「ん?」という方は、こちら。 )
すなわち、
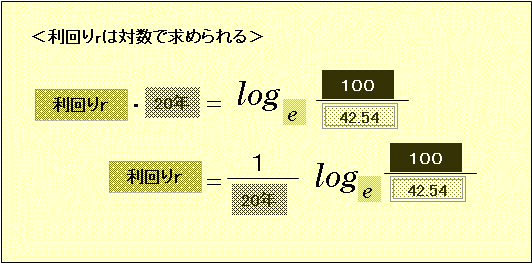
という形です。
この「e」なる値を底とする対数は自然対数という名称がついたスペシャルな対数で、通常は「e」という底の文字は省略されるか、あるいは、他の一般の対数logとは一線を画して「ln」という記号を用います。
この式の値は、関数電卓やExcelの関数機能(ln関数)ですぐに計算することができます。
そこで出てきた値0.8547を「期間=20」で割ると、年利回りrは4.27%です。
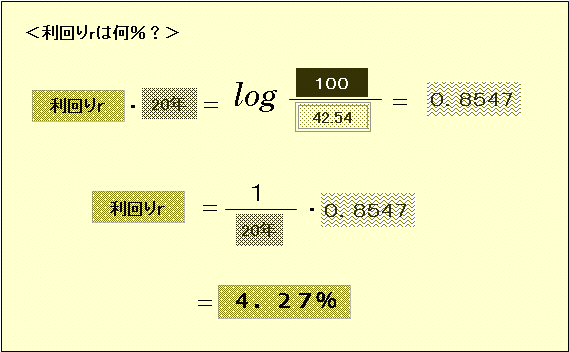
この「毎日複利で増えていく」という様子をグラフにしてみましょう。
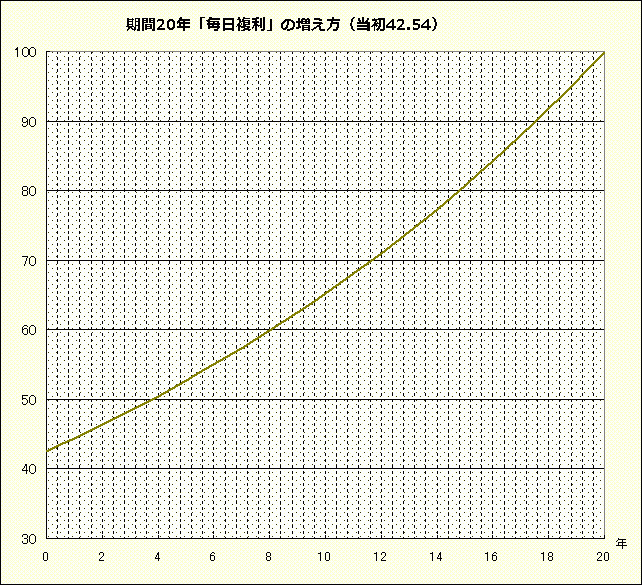
このグラフのどこの期間の部分を切り取っても、増え方は一定率です。
現実には、償還までの間の債券価格はその時々の金利情勢や市場の需給によって変化するので、こうした曲線を描くことはありませんが、ゼロクーポン債を「毎日複利で増え続ける」と捉えると、その元本はこんなふうに着々と成長していく形になります。
先述したように、年複利回数をもっと大きくしても、計算される年利回りはこの「毎日複利の年利回り」4.27%と変わりません。つまり、1時間複利でも、1秒複利でも、0.001秒複利で増えると考えても、年利回りは4.27%ということです。そうすると、デフォルトさえしなければ、このゼロクーポン債は償還までの間、それこそアメーバのごとく年利4.27%で時々刻々複利で元本を増殖させている債券、とも言うことができます。
【ゼロクーポン債】もしも、毎日複利で元本が増えているとしたら…。は以上です。