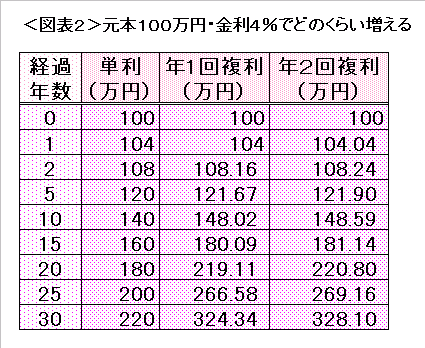
(2)毎日複利で増えたとしたら、“巨万の富”になるのか?
本書でも紹介しているように、円建て債券の利回り表示は単利が一般的ですが、外債の場合には複利表示のほうが多くなっています。
その複利表示も、米国債は年2回複利、欧州(大陸)債は年1回複利の表示であるなど、国・地域の慣習的なものによって違いがあります。
(ちなみに、利回り表示や経過利息計算などの際、1年を何日として計算するかも国・地域によって異なります。日本は365日ですが、1年を360日 とか、前回利払い日から次回利払い日までの「実日数」、として計算するところもあります。)
本書の記述の中では、米国債(主にゼロクーポン債)は基本的には年2回複利としているのですが、年2回複利となると、年1回複利よりもさらに増えるパワーは大きくなります。

年2回複利の場合、年1回複利の式の「金利」を2で割り、指数の「年数」に2を掛けると元利合計額が出てきます。
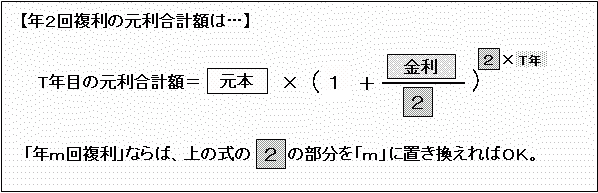
本書の「毎月分配型ファンドの再投資」のところで、「年12回複利」の結果を出していますが、年複利回数が4回ならば、上の式の「2」の部分にを「4」に、年12回複利なら 「12」に置き換えて計算します。
年2回複利の場合、年1回複利の「1+金利(=年利)」の部分が、「1+(金利/2)」と小さくなります。年利4%なら、年1回複利の「1+金利」は1.04ですが、年2回複利は「1.02」です。
反面、年1回複利ならば「年数T」だけだった指数の部分が、年2回複利ならば「2×年数」と大きくなります。
これが、年複利回数が増えると元利合計額も大きくなる要因なのですが、では、年複利回数をもっともっと多くしたら、たとえば毎日複利で増えるとしたら、元利合計額はどれだけ伸びていくのでしょうか。
毎日複利で増えるとしたら、それこそ雪だるま式に残高がどんどん増えて、巨万の富になるのではないか、という気がしないでもありません。
ところが、年複利回数を多くしていくと、次第に残高の伸び方は鈍くなっていきます。
年複利回数が100回(およそ週2回複利)を超えるくらいになると、それ以上いくら複利回数が増えても残高はほとんど変わらなくなってしまうのです。
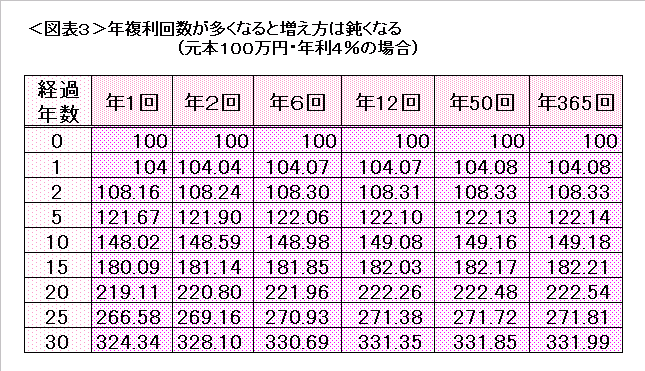
実は、年複利回数をどんどん大きくしていくと、年利4%の場合の30年後の元利合計額は「332万117円」にどんどん近づき、それ以上は頭打ちです。
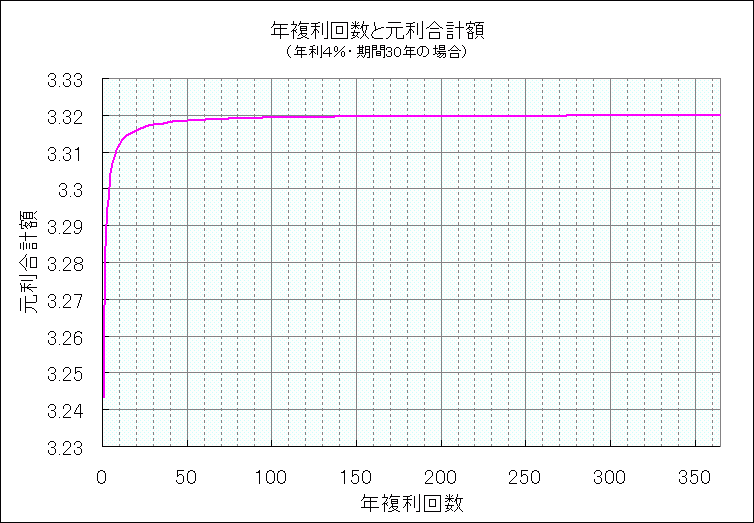
この例に限らず、たとえば年利をrとすると、年複利回数が大きくしていった場合、T年後の元利合計額は元本×2.7182818のrT乗で表される“定額”に近づき、それ以上はほとんど増えなくなるのです。
※「何故そうなるんだ」「この『2.71828』という数字は一体何?」という方はこちら。(年複利回数が大きくなると残高が”定額”に近づく理由とは)
と、いうふうに聞くと、たとえば日掛け金融で借金をして、毎日毎日複利で金利を計算されても「借金残高は雪だるま式には増えたりはせずに、どこかで“定額”になる んじゃないか」という印象を持つかもしれません。
確かに、年複利回数が非常に大きくなった場合、「とある○年後」の残高が複利効果でより増える作用は薄れます。
ただし、元本×2.7182818のrT乗の式の「rT乗」の部分が大きくなれば、残高の額自体はそれとともに増えていきます。よって、期間T年が長くなれば、借金残高はやはり雪だるま式にどんどん増えることに変わりはありません。
【複利】年複利回数が大きくなると残高はどれだけ増えるのかは、以上です。