(1)単利と複利。年数によって増え方はこんなふうに違ってくる
本書で「中長期的に元本を成長させたいのであれば、複利で増やせる対象を選ぶことが大きなポイント」と述べています。
金利による残高の増え方の計算方法としては、単利計算と複利計算とがあります。
おそらく、「単利と複利なんて、今さら言われなくてもよく知ってますから」という人が多数だと思います。
ところが、単利はともかくとして、複利に関しては非常に面白い面が多々あります。それを知っていれば大金持ちになれる、ということではありませんが、知っていて損はありません。
というわけで、知っているようで知らない(かもしれない)「複利」の側面を取り上げてみます。
まず、単利と複利(年1回)は、

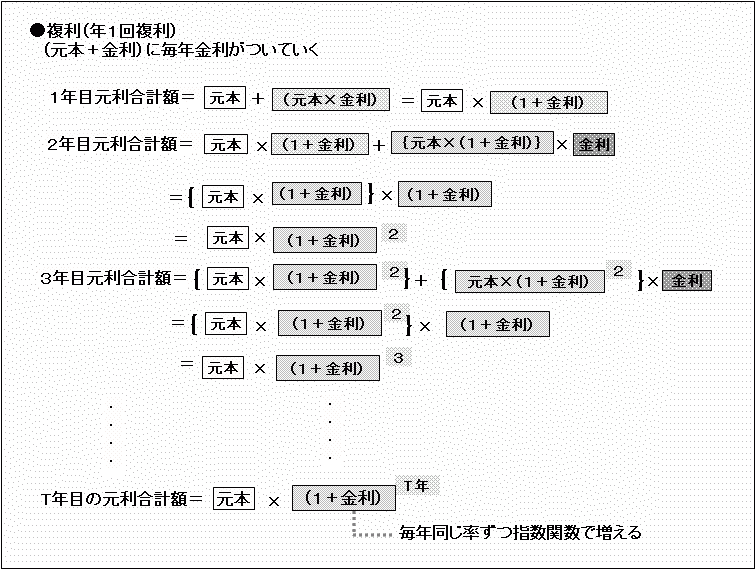
で計算されます。
上の式を見れば分かる通り、単利は「年数が経過するごとに、当初の元本が定額ずつ増えていく」という掛け算です。金利をr、年数をTとすれば、金利で増える額は「元本×r」のT倍ということになります。
これに対して複利は、年数が経過するごとに、当初の元本は定率ずつ増えていきます。元本は「1+r」の定率ずつ増える、つまり「1+r」のT乗という指数関数です。
指数関数といえば、高校の数学Ⅱでやったと思いますが、「その後、指数関数なんて使ったことはありません!」という人もいるのではないでしょうか。
確かに、たとえば「2乗」なら面積の計算、「3乗」ならば体積計算などで使う機会があるとしても、4乗、5乗、ましては10乗や30乗などというもの、一体何に使うのか。理工系に行った人でなければ使う機会などほとんどないだろう、と思えるかもしれません。
が、実は「複利」という、お金を預貯金に預けている人なら誰にとっても身近なところで、4乗なり5乗なり、10乗なり、という指数関数が活躍するわけです。(指数関数に限らず、高校の数学は金利や債券価格に関連する計算で大いに使われます。)
ちなみに、表計算ソフト『Excel』で指数計算をするときには、「^」を使います。
たとえば、「金利3%の年1回複利」であれば、5年後の元利合計額は、「=元本額*(テンキーの掛ける)1.03^5」と入力すれば出てきます。
ここで、同じ元本額からスタートして、単利と複利でどのくらいの差になるのかを見てみましょう。
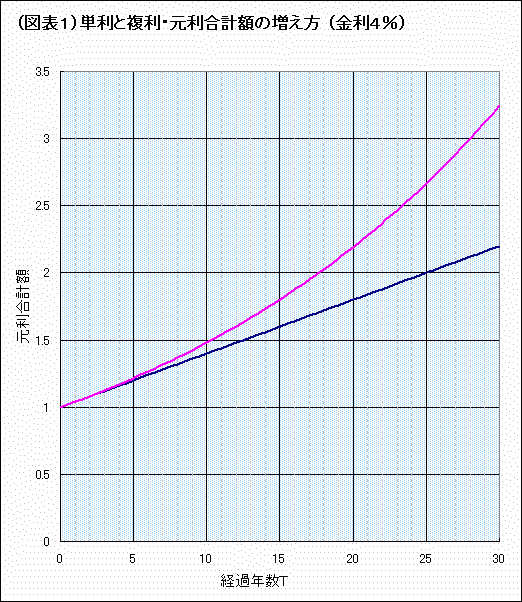
図1のグラフは、金利が4%の場合、元利合計額が年数経過とともにどう増えていくかを示したものです。
1年後時点では、単利も複利も同額です。
このことは、単利と複利の式からもわかります。式中の「T」に「1」を代入すれば、どちらの式も全く同じ形です。
1年後以降、年数が経てば経つほど複利の伸び方が大きくなり、元利合計額の差はどんどん広がっていきます。
たとえば、2年後では、単利が元本の1.08倍、複利は元本の1.0816倍と、大した差ではありませんが、10年後は単利が元本の1.4倍、複利は1.48倍。30年後ともなれば、単利が2.2倍に対して、複利は3.2倍と、元本額は3倍以上に増えています。
指数は英語で「Power Number」と言いますが、これを見ると、確かに指数関数的に伸びる複利はパワーがある、という感じがするのではないでしょうか。
ところで、同じ元本額でスタートしたということは、「T=0」では単利と複利は当然同額。そして1年後(T=1)もまた単利と複利は同額です。
ということは、T=0からT=1までの間というのは一体どういうことになっているのでしょうか。
仮に日割りベースでも単利・複利で計算するとすれば、T=0からT=1の間は、単利のほうが元利合計額は多くなります。
たとえば、T=0.5(6ヶ月)の場合、単利は
1+(0.04×0.5年)=1.02
ですが、複利は
(1+0.04)0.5年=1.0198
と、わずかではありますが、0<T<1の範囲では“掛け算”のほうが指数関数よりも有利になります。
※「0.5乗というのは一体何?」という方はココをクリック。
次は、(2)毎日複利で増えたとしたら、“巨万の富”になるのか?、です。