(1)まず、「円ベースの利払い金率」から考えてみる
外貨投資では、外貨を円に換えるときに当初よりも円高になっていると円換算金額が目減りしてしまいます。
外貨建て債券ならば、償還時の為替レートが購入時のレートよりも円高ならば円換算で“元本割れ償還”です。
が、本書でも述べているとおり、債券の金利分が償還時の為替差損をカバーする役割を果たします。
その「金利分でどのくらいの為替差損をカバーできるか」は、ゼロクーポン債ならば簡単に計算できます。
たとえば、償還価格100に対して債券価格70の米国ゼロクーポン債の場合、当初のレートが1ドル=85円とすると、
当初レート85円×債券価格70=償還時レート×償還価格100
を満たす償還時レートを求めればいいわけです。
計算すると、
償還時レート=当初レート85円×債券価格70÷償還価格100
= 59.5円
と出てきます。
利付債の場合は、計算が少々複雑になります。本書のほうでは掲載できなかったので(編集ご担当者から「載せるのは止めておこう」と言われてしまい…)、このサイトで紹介します。
利付債の「損益ゼロになる為替レート」は、償還までに受け取る利払い金の円換算金額合計が、円高による償還差損分のマイナスが等しくなるレートです。
この「利払い金の円換算金額」は、各利払い時の為替レートがいくらになるかによって違ってきます。これは事前にはわかりませんから、取りあえず、本書の中で紹介したように、「定額ずつ円高になる」という状況を想定してみます。
実際には「きっちり定額ずつ円高になる」などということはあり得ませんが、このやり方でもある程度の目安はつけられます。
まず、為替レートと円換算の利払い金の関係を抑えておきましょう。
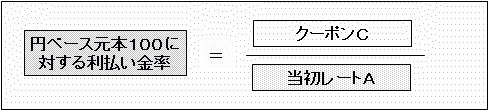
当初の為替レートをAとして、これを「円ベースの元本100」と考えます。
外貨ベースの表面利率をC%とすると、「当初レートAに対する表面利率C%」と、「円ベース元本100に対する円ベースの利払い金率」との関係は、
当初レートA:表面利率C(%)=円ベース元本100:円ベース利払い金率
となります。
その昔習った「外項の積=内項の積」を使うと、
当初レートA×円ベース利払い金率=表面利率C(%)×円ベース元本100
です。
右辺の「表面利率C(%)×100」は「C」の値(クーポン)そのものに置き換えられるので、円ベース利払い金率は、

で表現できます。
これに各利払い時の為替レートを掛ければ、その時々の利払い額が「円ベース元本100に対していくらに相当するか」が出てきます。
たとえば、外貨ベース元本100に対するクーポンが5、ある利払い時の為替レートは当初の1ドル=85円のままであれば、

利払い時の為替レートが1ドル=80円と円高になっていた場合には

といった具合です。なお、利払いが年2回の場合は、各利払い時に受け取る利金は「クーポンC」の半額になります。よって、上の式の「クーポンC」の部分を「C/2」として計算します。
次は、(2)「為替差損分=受け取り利払い分」となるレートとは、です。