
(2)「為替差損分=受け取り利払い分」となるレートとは
利付債の損益がゼロになる償還時レートとは、「為替レートがいくらであれば、償還時の為替差損分と、受け取った利払い金分とが同額になるか」ということです。
つまり、償還時の為替レートをたとえばXとして「為替差損分=受け取り利払い分」という等式を立てて、これをXについて解けば出てくることになります。
まずは、為替差損分から考えていきましょう。
当初レートをA、償還時のレートをXとすると、単位通貨あたりの償還時の為替差損は「A−X」です。
この為替差損「A―X」が、当初レートAを「円ベース元本100」としたとき、その何%に相当するか、言わば「円ベースの差損率」は、
当初レートA:為替差損分(A−X)=円ベース元本100:円ベース差損率
という比で考えるとわかります。
これも「外項の積=内項の積」を使えば、「当初レートA×円ベース差損率=為替差損分(A−X)×円ベース元本100」となるので、円ベース差損率は

という表現になります。
たとえば、当初レートが1ドル=85円、償還時に1ドル=70円の円高になっていたとすれば、円ベース元本100に対する差損は、

17.647(%)です。
次は、受け取り利払い額の合計を出してみます。
先述したように、円換算の受け取り利払い額はその時々の為替レートによって違ってきますが、取りあえず「定額ずつ円高になっていく」と想定します。
たとえば、償還までの期間が10年、利払い回数が年1回で、当初1ドル=85円だったレートが、償還時に1ドル=70円と、15円円高になったとします。
利払い回数は10年間で10回ありますから、この場合は、各利払い時の為替レートは1.5円ずつ円高になる、という想定になります。
ここで、何ということもなく「1.5円ずつ円高になる」と決めつけてしまいましたが、何故に「1.5円ずつ」なのかといえば、言うまでもなく
利払い1回あたりの円高額=(当初85円−償還時70円)÷利払い回数10回
だからにほかなりません。
そうすると、各利払い時の適用レートは、1回目の利払い時には当初レートから1.5円円高、2回目の利払い時はさらに1.5円円高のレートになりますから、当初レートよりも3円円高、3回目の利払い時は、さらに1.5円円高なので当初レートよりも4.5円円高…、といった具合になります。
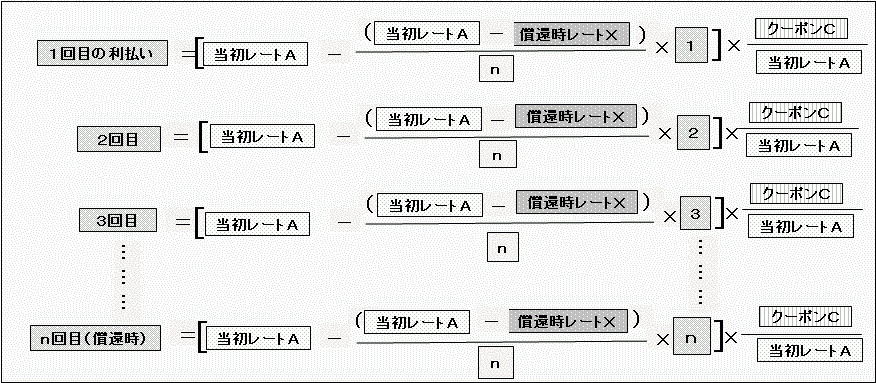
当初レートをA、償還時レートをX、利払い回数合計をn回としてまとめると、各利払い時の想定為替レートは、

です。
この各利払い金が「円ベース元本100のの何%に当たるのか」は、各利払い時の適用レートに前ページで出した「円ベース利払い率C/A」を掛ければ出てきます。
たとえば、外貨ベースのクーポンが3、年1回利払いで当初レートが1ドル=85円とすると、円ベースの元本100に対する受け取り利払い分(%)は、
・ 1回目の利払い=(85円−1.5円)×(3/85)=2.947(%)
・ 2回目の利払い=(85円−3円)×(3/85)=2.894(%)
といった具合になります。
各利払い時の受け取り分を全部合計したものが、「円ベース元本100に対する受け取り利払い合計」です。
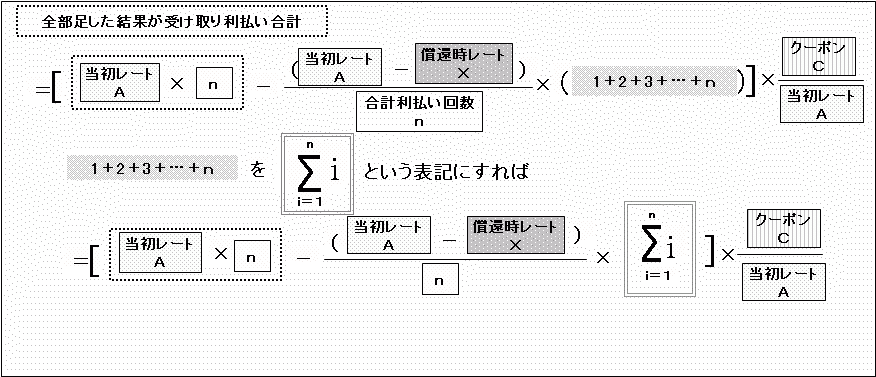
ちなみに、「Σi」(シグマ)などというものが出ていますが、これはiのところに1からnまで順番に入れて「1+2+3+…+n」という足し算をする、という意味の単なる“マーク”のようなものと考えてください。
先にも述べたように、利払いが年2回の場合は、上の式の「クーポンC」の部分を半額の「C/2」にします。
↑ Top へ戻る。