(3)利付債は「受け取るお金」を現在価値に直して合計する
利付債では、償還までの間に受け取る各利払い時のクーポンと、償還時に戻る額面金額それぞれを現在価値に直し、それを全部合計したものが債券価格(現在価値)になります。
とはいえ、単利で考える場合には、利払い1回ごとのクーポンや償還金額の現在価値をそれぞれ出して合計する必要はありません。
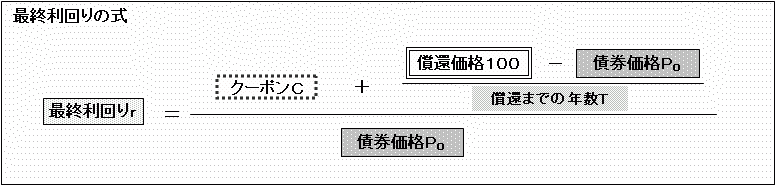
本書の巻末にも示してある「最終利回りの式」、

から、債券価格P0を求めればOKです。

という式です。
利払いが年2回以上ある場合も、結局は上式と同じになります。
年間のクーポン(表面利率)が額面100に対して4(%)、償還までの期間5年、償還価格100、年利回り3.5%の場合なら、
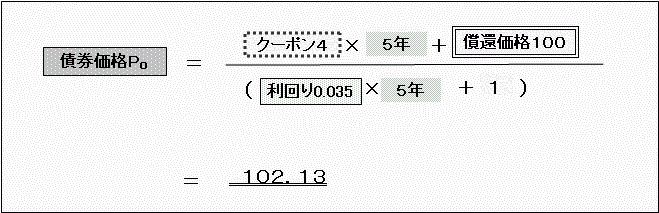
で、債券価格は102.13と出てきます。
ちなみにこの利付債、表面利率4%に対して、年利回りは3.5%とそれよりも低いということは、債券価格が額面価格100よりも高いことを意味するものでもあります。
複利の場合は、少々計算が面倒になります。
取りあえず、年1回利払いの例で考えていきましょう。
クーポンが額面100に対して4、償還までの期間5年、償還価格100、年利回り3.5%とします。
最初の利払い日がちょうど1年後とします。以後、1年経つごとに利払いがあり、5年後の償還時には、5回目の利払いと、償還金を受け取ります。
1年後の第1回目の利払い時にもらうクーポン「4」をC1とすると、その現在価値は、

です。
2回目のクーポンC2は「3.5%で年1回複利運用して、2年後に『4』になった」と捉えます。
そうすると、この2回目のクーポンの現在価値は、

と、1回目のクーポンC1よりも安くなります。
同じように、3回目、4回目、5回目のクーポンの現在価値を計算します。
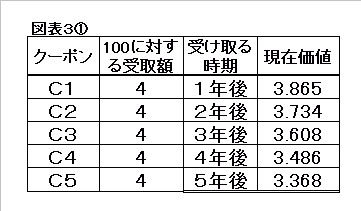
そして、償還時に戻ってくる償還価格100は、「3.5%で年1回複利運用して、5年後に『100』になった」、すなわち、
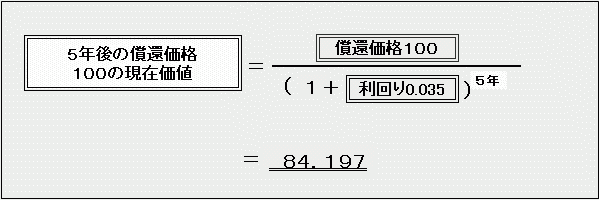
です。
これらを全部足したものが、この債券の価格(現在価値)になります。
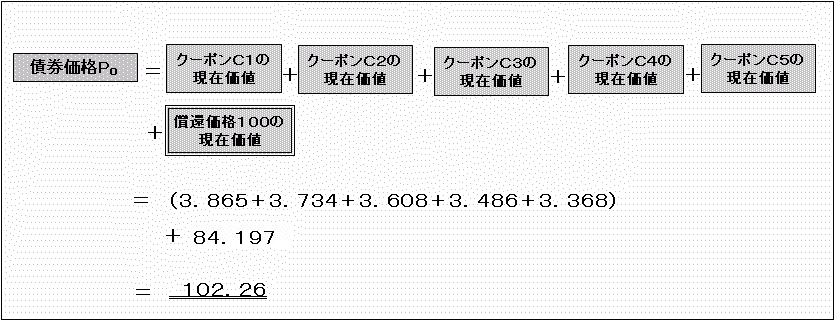
償還までの年数をT、各年のクーポンをC1、C2……CT、年1回複利利回りをrとして式にまとめると、、
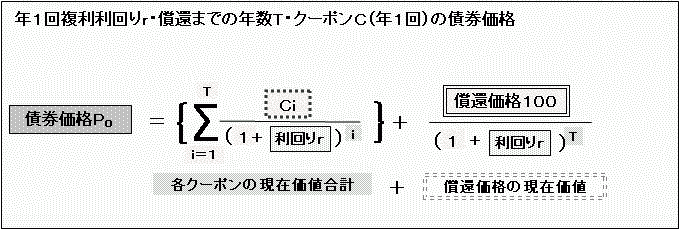
と表現できます。
ここでまた「Σ」なるものが出てきましたが、この記号は「『i』のところに1からTまでの数を入れて計算した各クーポンの現在価値を全部足す」を意味します。
年2回複利で考えるときには、年間のクーポンを半額にして、利回りrの部分を「r/2」に、期間Tの指数部分を「2×T」とします。
クーポンが額面100に対して4、償還までの期間5年、償還価格100、年利回り3.5%の利付債の場合、年2回複利換算の債券価格は、
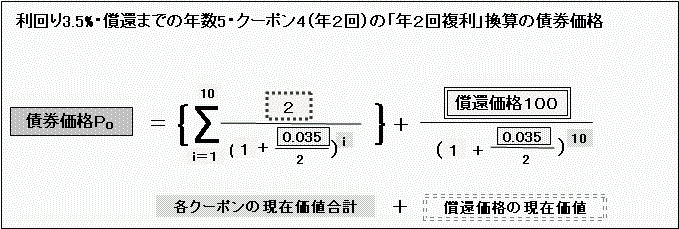
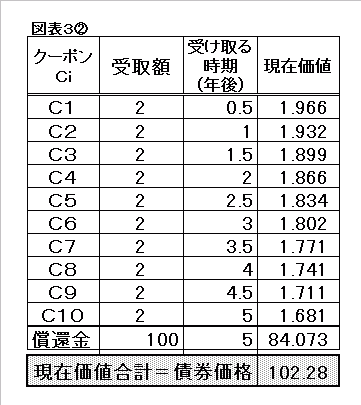
債券価格は102.28となります。
なお、この例のように、利回りが表面利率(クーポン)よりも低い(つまり、債券価格が償還価格よりも高く、償還差損が出る)利付債は、単利換算のほうが複利換算よりも債券価格は安くなります。
また、年1回複利換算複利のほうが年2回複利換算よりも債券価格の数字は安く出ます。
逆に、利回りが表面利率よりも高い(つまり、債券価格が償還価格よりも安く、償還差益が出る)利付債の場合は、単利換算のほうが複利換算よりも債券価格は高く、また、年1回複利のほうが年2回複利よりも高くなります。
【債券価格】「これから受け取るお金」の“いまの価値”はいくらかは、以上です。