(2)利回りをもとにゼロクーポン債の価格を出してみる
債券の利回りは、日本では通常単利表示になっていますが、米国債は年2回複利換算で利回りを表示しています。
利回りが複利であれば、「将来受け取るお金」を現在価値に置き換えて債券価格を求める際も複利で計算します。
本書の「期間が長いほど、債券価格は金利に敏感に反応する」のところで、利回り水準の変動による債券価格の変動率の例を紹介していますが、これも年2回複利の計算値です。
償還までの間定期的にクーポンを受け取る利付債と、クーポンのない割引債とでは、債券価格(=現在価値)の計算の仕方は異なります。まずは、仕組みがわかりやすいゼロクーポン債を考えていきましょう。
ゼロクーポン債は、利払いがない分、額面100よりも割り引かれた価格で発行されます。逆からいえば、この割り引かれた債券価格が元本となり、それが年2回複利運用されて償還時に100になる、という 形です。
債券価格をP0として、年利回り4%、償還までの期間が10年の場合なら、

という式で表されます。
この式をP0について解けば、それがイコールこのゼロクーポン債の債券価格(=現在価値)になります。

です。
年m回複利利回りをr、償還までの年数をTとすれば、ゼロクーポン債の債券価格(=現在価値)は、
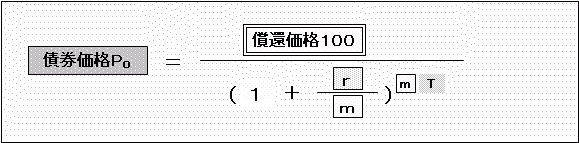
「『0.5乗』とはどういう意味なのか」の中に出てきた指数法則その4「×乗分の1=マイナス×乗」を使うと、これは

とも表せます。債券価格と償還価格100を入れ替えて、「年複利回数×年数」の指数部分にマイナスをつけるだけなので、式の形もシンプル、パソコンで式を入力するの際もこのほうがラクだと思います。
償還までの年数Tが大きくなると、右辺の分母が大きくなる、つまり、左辺の値は小さくなります。期間の長い債券ほど価格は安くなる、というわけです。
ところで、本書巻末の「単利と複利」のところで、元本金額とある年数後の元利合計額が同じ場合、単利換算すると利回りの数字は複利より高く出てくる、と述べています。
ということは、利回り・償還価格・期間が同じゼロクーポン債でも、単利で計算した場合と、複利で計算した場合とでは、債券価格が違ってくることになります。
先のゼロクーポン債の価格を単利で計算すると、

です。
年2回複利で計算したときよりも、債券価格が高くなっています。
そうすると、「同じ債券でなのに、単利で計算されていると高く買わされるのはおかしいんじゃないか」とも思えてくるかもしれません。
が、この単利で計算したゼロクーポン債と、先の年2回複利で計算したゼロクーポン債は「同じ」ではないのです。
この単利で計算したゼロクーポン債は、「71.43の元本が年4%で単利運用されて10年後に100になる」という債券です。これと同じ債券を年2回複利で換算したときの利回りrは
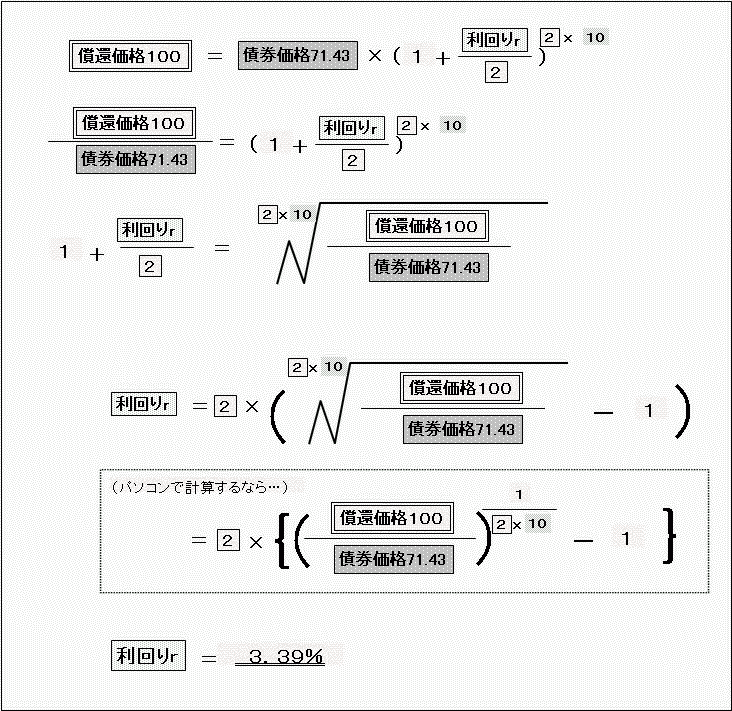
と、3.39%です。
(「20分の1乗」とは何? という方はこちら。
つまり、この債券は、先の例の「年2回複利で利回り4%」のゼロクーポン債よりも低い利回りの債券というわけです。
また、先の例の「年2回複利で利回り4%」の債券は、単利換算すると、
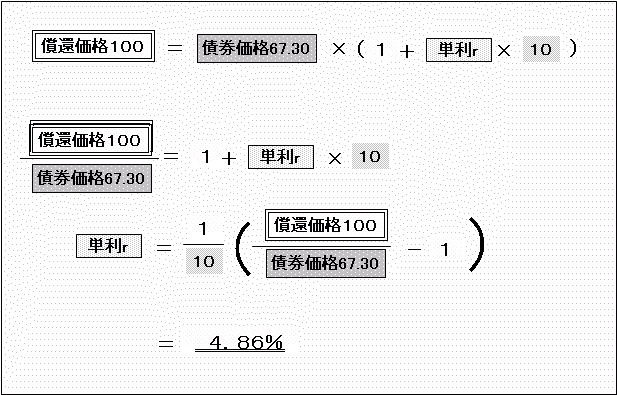
つまり、単利換算の利回り4.86%の債券が、先の例と「同じ債券」です。
次は、(3)利付債は「受け取るお金」を現在価値に直して合計する、です。