(2)利回りの変化に対する「債券価格の反応度合い」を知る方法
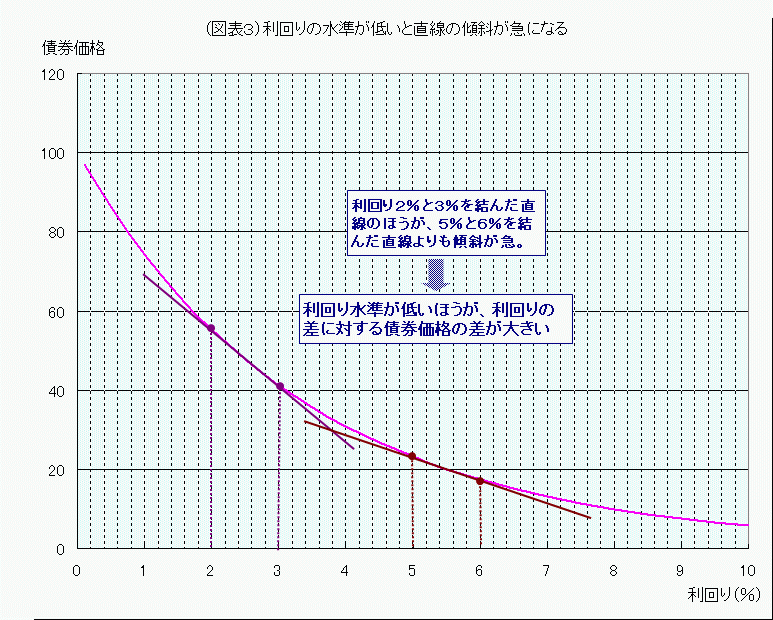
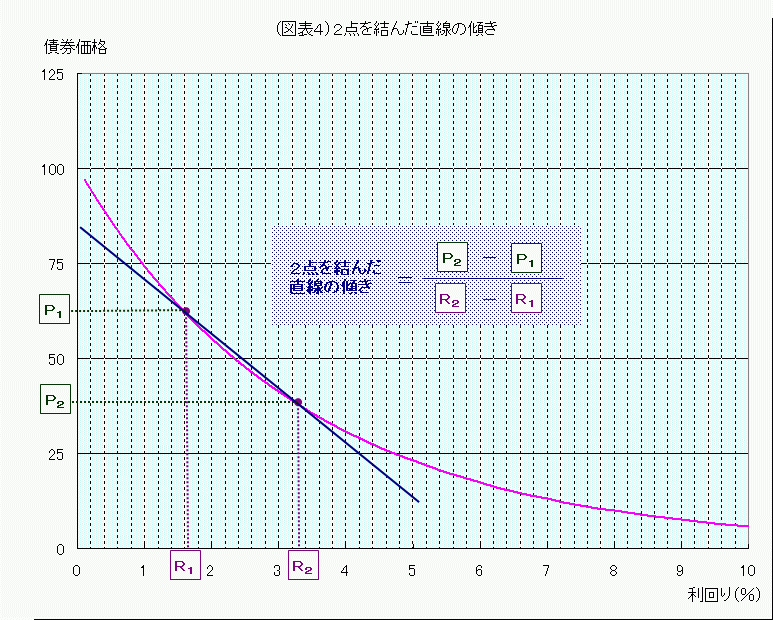
ところで、利回りと債券価格のグラフの中の「2つの点を結んだ直線の傾きの度合い」は、同じ1%の利回りの差でも、たとえば利回り2%と3%を結んだ直線と、5%と6%のを結んだ直線とは、同じではなさそうです。
期間5年のグラフではちょっとわかりにくいのですが、期間30年のグラフで「2%と3%」「5%と6%」の点を結んだ直線を引いてみると、確かに傾き方は違っています。

「2%と3%」を結んだ直線のほうが傾き方が急になっている、ということは、同じ期間30年のゼロクーポン債で同じ利回り差1%でも、利回り水準が低いときのほうが、債券価格の変動度合いが大きいということです。
この「2点を結んだ直線の傾き」の値は、利回りR1のときの債券価格をP1、利回りR2のときの債券価格をP2とすると、
という式で表されます。
期間をTとすると、P1、P2は、
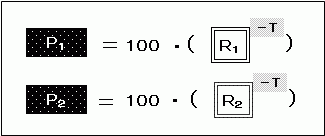
となりますから、この2点を結んだ直線の傾きは
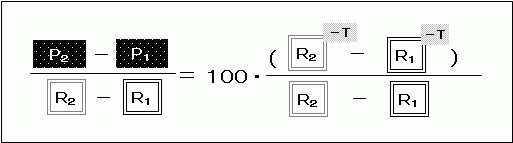
です。
この式を少し変形すると、「2点を結んだ直線の傾き」は利回り水準の低いときのほうが大きくなることがわかります。
「RマイナスT乗」を「『RのT乗』分の1」に書き換えてみると、
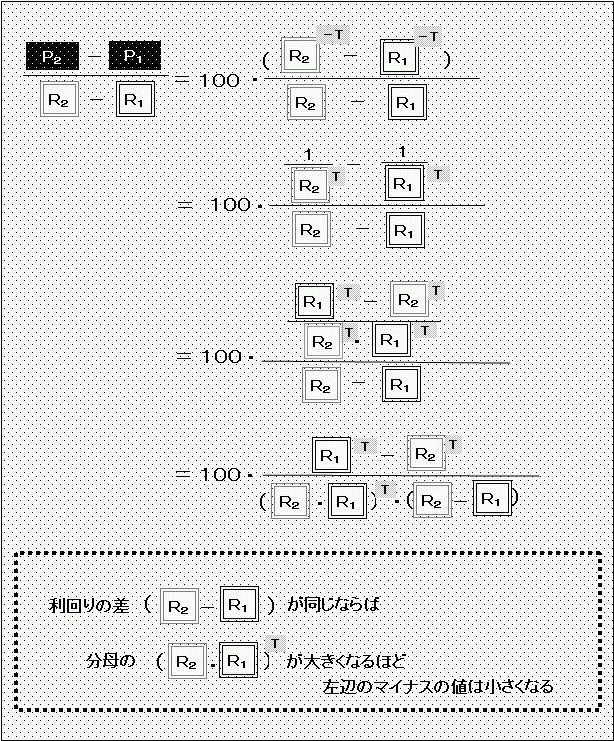
となり、期間が同じで場合、利回りの差が同じでも、利回りの水準が高いときのほうが右辺の分母が大きくなることがわかります。すなわち、左辺のマイナスの値は小さくなる、ということです。
期間30年で「R1=1.02、R2=1.03」のケースと、「R1=1.05、R2=1.06」の値を出してみると、
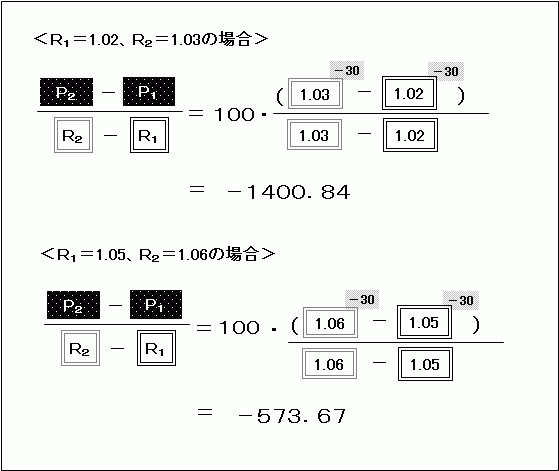
と、確かに「R1=2%、R2=3%」のほうがマイナスの値は大きくなっています。
この式を活用すれば、その時々の利回りの水準に応じた「利回りの差に対する債券価格の反応度合い」を知ることができます。
それにしても、傾きの値がずいぶんと大きなマイナスですが、これは、R2とR1の差0.01で割っているからで、たとえば金利差1(%)で割れば、傾きの値はこの計算結果の100分の1になります。
次は、(3)利回りの差を極小にすると「債券価格の金利感応度」がわかる、です。