(1)期間が長いほど金利の変化に対して敏感に反応する
本書の中で何度か紹介しているように、債券の価格と利回りは、「一方が上がれば、もう一方は下がる」というシーソーのような関係にあります。
この「利回りと債券価格の関係」、そして、その関係は償還までの期間によってどう違ってくるのかをもう少し掘り下げてみましょう。
期間5年と期間30年の割引債(ゼロクーポン債)で考えてみます。
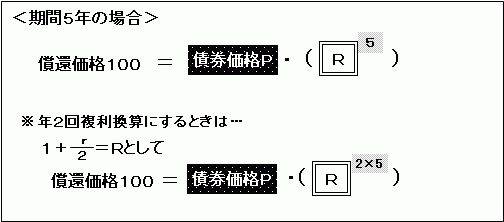
ゼロクーポン債は債券価格100で償還します。期間5年ならば、「いまの債券価格が5年後には100になる」ということです。
いまの債券価格をP、「1+いまの利回りr」をRとすると、

という式になります。
(この式では、年1回複利にしていますが、米国ゼロクーポン債などは年2回複利として計算するのが通常です。)
そうすると、いまの債券価格Pは、
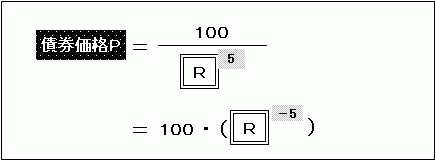
で表されます。
この式で、「Rの5乗分の1」を「Rのマイナス5乗」に書き換えていますが、この書き方のほうがシンプルなので、以下では「Rの×乗分の1」を「Rのマイナス×乗」と書くことにします。
※ なぜ「RのT乗分の1」が「RのマイナスT乗」になるのかは、「0.5乗とは一体どういう意味なのか」、をご覧ください。
利回りrが2.5%ならば、この式のRに「1.025」を入れます。

債券価格は、88.3854と出てきました。
一方、期間30年のゼロクーポン債の債券価格は

という式になります。
期間5年のゼロクーポン債が利回り 2.5%のとき、期間30年のゼロクーポン債の利回りはどのくらいかは、その時々の市場参加者の先行き観測や需給によって違ってきますが、4月12日現在の米国ゼロクーポン債でいうと、期間約5年の利回りが2.3%、期間約30年で4.9%程度です。
この水準に合わせて、期間30年の利回りを5%としてみましょう。先ほどの式のRに1.05を入れると、

債券価格は23.1377です。
ちなみに、これは「30年後の100が、いまなら23少々で買える」という意味ですが、いかにも安い! という感じがするのではないでしょうか。
では、利回りがそれぞれ1%ずつ高い場合、債券価格はいくらになるでしょうか。
期間5年で利回りがプラス1%の3.5%とすると、先ほどの式のRの部分が1.035になるので、

と、債券価格は84.2973に下がります。
利回り2.5%の債券価格に比べると4.74%安くなっています。
期間30年で利回りがプラス1%の6%ではどうなるでしょうか。

債券価格は17.4110です。
利回り5%のときの23.1377も「かなり安い」という感じがしましたが、利回り6%となると、それよりも約25%安く買える、というわけです。
本書の中でも紹介していますが、このように、償還までの期間が長くなると、利回りの変化に対する債券価格の反応が大きくなります。
このことは、利回りと債券価格の関係をグラフにしてみるとよくわかります。
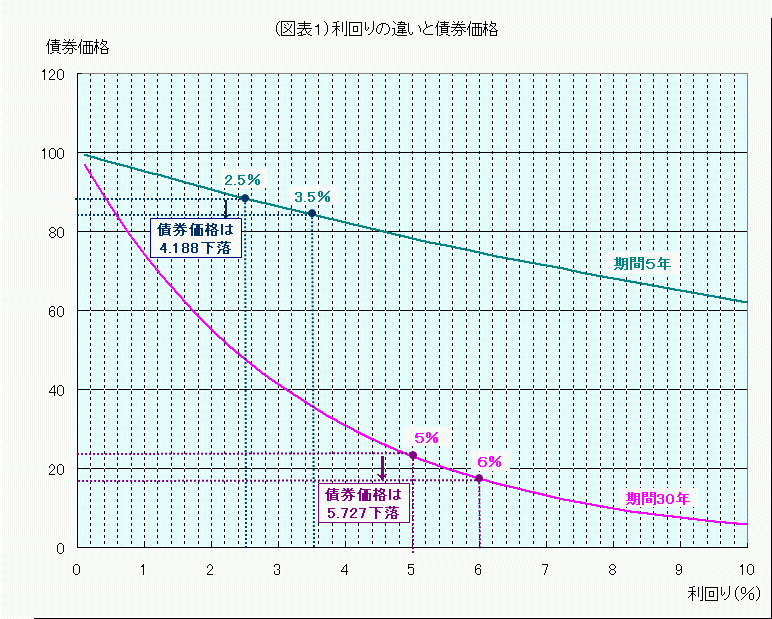
期間5年のほうは、利回り2.5%と3.5%の1%の差がもたらす債券価格の差は4.188。
これに対して、期間30年では、利回り5%と6%の1%の差が、債券価格に5.727の差を生じさせています。
この「4.188」「5.727」という債券価格の差を、Rの差0.01(金利差1%)で割った値は、それぞれ2点を結んだ直線の傾きを示します。
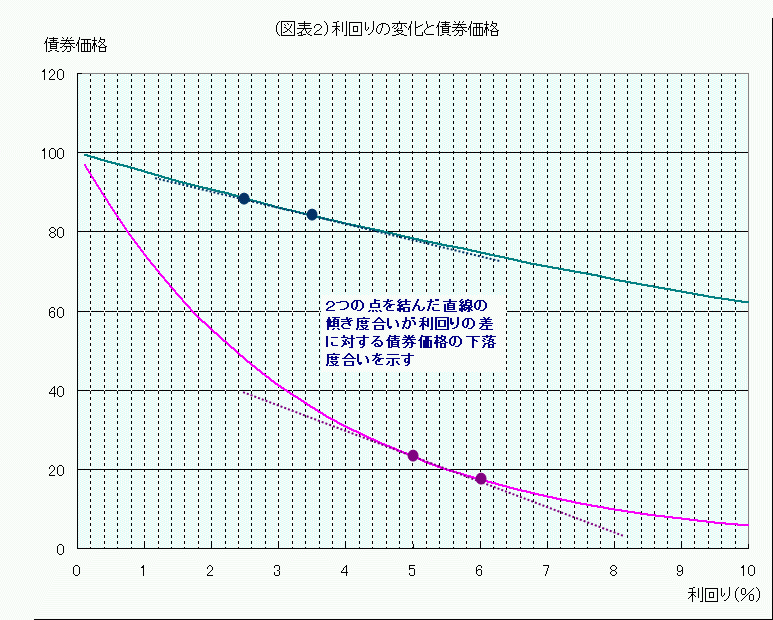
利回りが高くなると債券価格は安くなりますから、2点を結んだ直線は右肩下がり、つまり「直線の傾き」はマイナスです。
このマイナスの値が大きく、右肩下がりの傾斜が急であるほど、金利上昇による債券価格の下げ方が大きいことを意味します。
言い換えると、2つの点を結んだ直線の傾き方は、「利回りの差に対する債券価格の変動の度合い」を表している、ということです。
次は、(2)利回りの変化に対する「債券価格の反応度合い」を知る方法、です。