はじめての人のための＜円建て＆外貨建て＞
『日本一やさしい　高利回り債券の見つけ方』

【債券価格】金利が上昇すると債券価格はどのくらい下がるのか

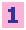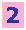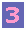
（３）利回りの差を極小にすると「債券価格の金利感応度」がわかる

利回りの変化が「極々わずか」と想定する

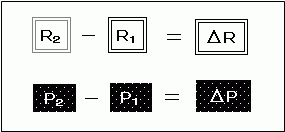
前ページでは２点の（１＋金利ｒ）の差を「Ｒ２−Ｒ１」、それに応じた債券価格の差を「Ｐ２−Ｐ２」としましたが、これを、

としてみます。この△は２つの量の差を表すときに用いられるもので、「デルタ」と読みます。

そうすると、Ｒ２は、

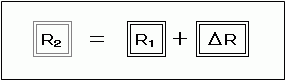
と表現できます。

これを用いて前ページの式を書き換えると、

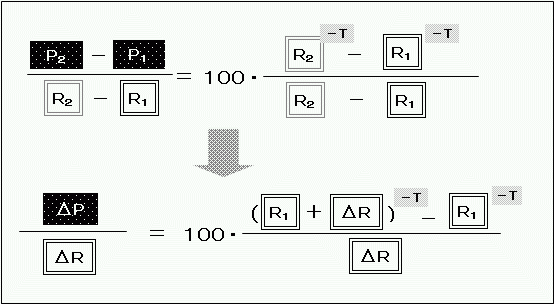
となります。

もし、２つの利回りＲ１とＲ２の差が極々わずかしかない、つまり、△Ｒの値が極小だとしたら、先ほどの「２点を結んだ直線」は、あたかも「Ｒ１という一点だけにタッチしている接線」といっても差し支えないような格好になるはずです。

とすると、この式で出てくる直線の傾きは、利回り２％なり、５％なり“ジャストスポット”における債券価格の反応度合いを示す、と考えて差し支えないことになります。

これは一体何かというと、これこそが高校の時に習った「微分」なるものにほかなりません。この「利回りの極々わずかな変化に対する、債券価格の反応度合い」を表す式を求めることが、「債券価格の式を『１＋利回り（金利）』のＲで微分する」ということです。

Ｒ１を単に「Ｒ」と書き換えて、かつて習ったような書き方をすると、

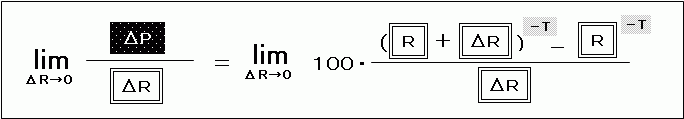
のようになります。

「lim」なる記号がありますが、これは「ΔＲを極限まで、ほとんどゼロと言っても差し支えないくらいに小さくする。だがしかし、完全なゼロではない」という意味です。

この式をせっせと計算することが、「債券価格Ｐを『１＋利回り（金利）』Ｒで微分する」という作業です。そして、この式をせっせと計算して出てきた結果は「導関数」と呼ばれます。

※「微分とはどういうものだったかな？」という方は、微分すると「変化の様子」が見えてくる、をご覧下さい。

「期間が長い債券ほど価格の金利感応度が高い」はこれで一目瞭然

かつて、y＝x² を x で微分すると ２x になる、y＝x³ を微分すると 3x² になる、といった具合に、「y＝xⁿ を x で微分すると nx^n-1 になる」という公式を覚えている人も多いと思います。これは、先ほどと同じような「Δｘ」が分母にある式をせっせと計算した結果です（正確には、せっせと計算した結果は「完全にこれらと同じ」ではなく、「これらと同じといっても差し支えない」ものになります）。

ｎ乗が負の値のときもこれと同じように、y＝x^-n を x で微分すると、

 -nx^-n-1

という式になります。

※「なぜ、そうなるのか」「さっきの式の分母にあった△Ｒはどうなるんだ」という方は、xⁿ を微分すると「n*x^n-1」になるのは何故？をご覧下さい。

これを用いると、債券価格を求める式 P = 100･R^-T をRで微分した結果は、

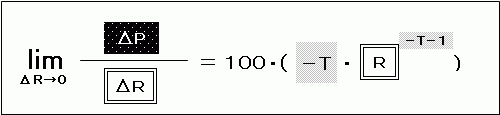
といった式で表現されます。

ここで「R^-T-1」に注目します。

「0.5乗とは一体どういう意味なのか」の中で紹介した指数法則その２を使えば、これは、

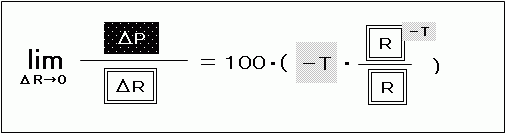
と同じです。

そうすると、先ほどの式は、

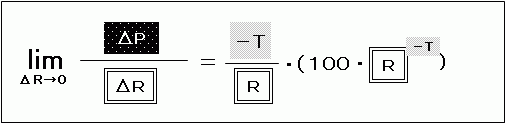
と書き換えられます。

この式の中に「100･R^-T」が入っていますが、これは微分する前の式と同じです。つまり、この部分は「利回りが変化する前の債券価格Ｐ」を表しているわけです。

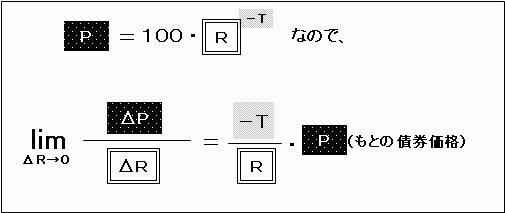
そうすると、ある利回り水準が（極々わずかに）変化したときの債券価格の変動度合いは、もとの債券価格に「−Ｔ／Ｒ」を掛けた値になります。これが、「利回りの（極々わずかな）変化に対する債券価格の感応度」を表す式です。

この式を見れば、「期間が長い債券は分子のＴが大きくなるので、債券価格がマイナスに動く度合いも大きくなる」、「期間が同じであれば、もとの利回り水準が高いほど分母のＲが大きくなるので、マイナスの値は小さくなる」ということがわかると思います。

数字を入れて計算してみるととんでもない結果に…

実際に、具体的な数字を入れて「利回りの変化に対する債券価格の感応度合い」を調べてみましょう。

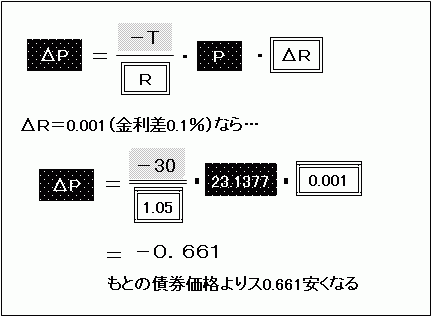
期間Ｔを30年として、利回り５％、すなわちＲ＝1.05を入れてみます。

この時点の債券価格Ｐは「100・（1.05）⁻³⁰」で23.1377ですから、

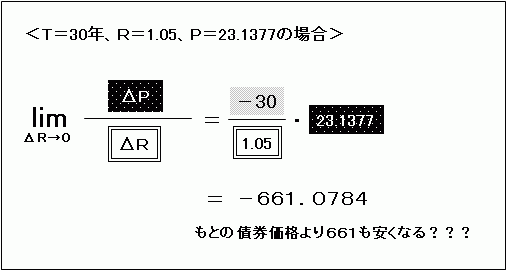
何と「−661.0784」というとんでもない数字が出てきてしまいました。どう考えても、「利回りが５％から変化したときの債券価格が、もとの債券価格よりも６６１．０７８４安くなる」などということはあり得ません。

一体どういうことでしょうか。

と、ここで式をよくよく見ると、この661.0784というのは、債券価格が動いた大きさ（変動幅）の△Ｐではなく、△Ｐを利回りの変化△Ｒで割った値です。

債券価格がどのくらい動くか、価格の差ΔＰを調べるのであれば、この−661.084に△Ｒを掛けなければなりません。

金利が５％から5.1％に変化したとすると、△Ｒは「1.051−1.05」の0.001です。これを−661.0784に掛けると、△Ｐはもとの債券価格よりも０．６６１安くなる、という結果になります。

利回りが５％のときと、5.1％のときの債券価格をそれぞれ計算してみると、

　　金利５％のとき　　　　Ｐ＝23.1377

　　金利５．１％のとき　　Ｐ＝22.4863

で、0.1％利回りが高いときの債券価格は、もとの債券価格よりも0.651安くなる計算です。まあ、先ほどの微分で出した結果とだいたいは合っています。。

なお、金利の差をもっともっと小さくして△Ｒを0.000001とすると、ほぼぴったりの計算結果になります。

【債券価格】「金利が上昇すると債券価格はどのくらい下がるのか は、以上です。