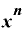 を微分すると「
を微分すると「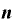 ・
・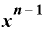 」になるのは何故?(1)
」になるのは何故?(1)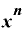 を微分すると「
を微分すると「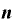 ・
・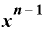 」になるのは何故?(1)
」になるのは何故?(1)
■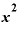 を微分すると「
を微分すると「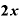 」になる理由は「
」になる理由は「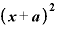 」の展開式の中に■
」の展開式の中に■
かつて微分なるものを習ったとき、おそらく唯一理解できたことはは、たとえば「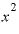 を微分すると
を微分すると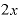 になる」とか「
になる」とか「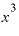 を微分すると
を微分すると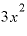 になる」とか、とにかく「
になる」とか、とにかく「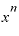 の微分というものは、nを前に出して、xの(n-1)乗に変えればいい」という、簡単に丸暗記できる公式だけでした。
の微分というものは、nを前に出して、xの(n-1)乗に変えればいい」という、簡単に丸暗記できる公式だけでした。
それにしても、一体なぜ、こんな機械的にやってしまえる公式になるのでしょうか。
「2xになるというのは、xを2乗しているのと何か関係があるんじゃないの?」と、なんとなく思った人もいるのではないでしょうか。
そう直感した人は天才です。まさしく、その通りなのです。
ここで、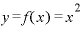 という関数を、微分の定義式に当てはめてみます。
という関数を、微分の定義式に当てはめてみます。
微分の定義式は、
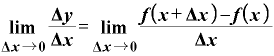 (1)
(1)
というものでした。
ここで重要なポイントは、「Δx」は限りなくゼロに近いけれども、完全にゼロではない、ということです。
なぜ完全にゼロにしないのかというと、これをゼロにしてしまうと、この割り算の答えを出すことができないからです。
分数で分母がゼロの場合、その値は∞に発散してして、特定できないのです。
それで完全にゼロにはしないのですが、ただし、限りなくゼロに近い、非常に小さい値です。
この(1)式に、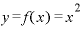 を当てはめるう場合、まず、(1)式の
を当てはめるう場合、まず、(1)式の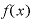 のところには「
のところには「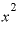 」を入れればいいことはすぐにわかると思います。
」を入れればいいことはすぐにわかると思います。
では、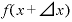 のところには何を入れればいいでしょうか。
のところには何を入れればいいでしょうか。
ここで改めて、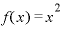 の意味を考えると、「x」とはいろいろな値をとる変数で、「
の意味を考えると、「x」とはいろいろな値をとる変数で、「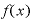 とは、xに当てはめる値を2乗する関数である」ということです。
とは、xに当てはめる値を2乗する関数である」ということです。
xに当てはめるものが、たとえば「1」だとすれば、()の中に「1」が入って、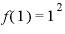 。xが「2」ならば、
。xが「2」ならば、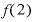 =
=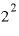 です。
です。
xに「a」を当てはめろというのであれば、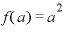 。「xは『a+b』だ」というなら、
。「xは『a+b』だ」というなら、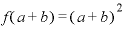 となります。
となります。
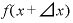 は、「xのところに『x+⊿x』を当てはめろ」ということですから、これは
は、「xのところに『x+⊿x』を当てはめろ」ということですから、これは
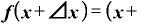 ⊿
⊿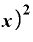
という式になります。
そうすると、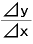 の部分は、
の部分は、
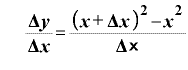 ……①
……①
ということです。
この⊿xをごくごく小さい値にしていくと、その答えはほとんど「2x」といっても差し支えない値になる、ということですが、それは一体なぜなのでしょうか。
ここで、中学のときに習った「展開式」を思い出してみます。
たとえば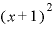 という式は、
という式は、
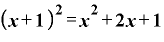
というふうに展開できるのでした。
「1」のところを「a」という文字で表せば、
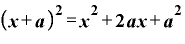
です。
この「a」のところを「⊿x」に置き換えてみれば、
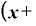 ⊿
⊿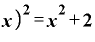 (⊿
(⊿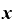 )・
)・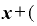 Δ
Δ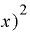
になります。
そうすると、①式の分子⊿yは、
⊿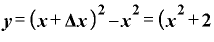 (⊿
(⊿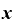 )・
)・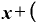 Δ
Δ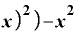
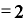 (⊿
(⊿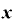 )・
)・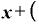 Δ
Δ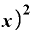
という形になります。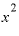 は差し引かれて消えてしまいました。
は差し引かれて消えてしまいました。
さらに、これをΔxで割ってみると、
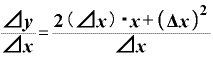
になりますが、分子の2つの項「2x(⊿x)」「((Δ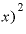 」は、どちらも⊿xが入っていますから、分母のΔxと約分できます。
」は、どちらも⊿xが入っていますから、分母のΔxと約分できます。
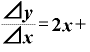 ⊿
⊿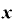 ……②
……②
と、約分によって分母のΔxをなくすことができるわけです。
この「分母のΔxが消える」というのは実に好都合です。
というのは、このΔxを「ほとんどゼロなんだが、ゼロではない」としていたのは、先述したとおり、分母をゼロとしてしまっては計算結果が特定できなくなるからです。
しかし、この約分によって、もはや分母のΔxは消え失せました。となれば、Δxは「もはやゼロ」として扱っても差し支えなくなります。
ということを念頭に、②式を改めて見てみると、「微分すると変化の様子が見えてくる!」の中で
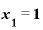 のとき、「yの差÷xの差」を計算すると、その答えは「2」+「xの差と同じ値」
のとき、「yの差÷xの差」を計算すると、その答えは「2」+「xの差と同じ値」
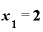 のときには、その答えは「4」+「xの差と同じ値」
のときには、その答えは「4」+「xの差と同じ値」
となったことが思い出されるのではないでしょうか。
そういう結果になった理由がまさに②式にあります。
すなわち、
・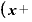 ⊿
⊿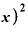 から
から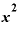 を引くと、
を引くと、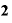 (⊿
(⊿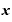 )・
)・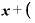 Δ
Δ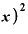 だけが残る。これがΔy。
だけが残る。これがΔy。
・これをΔxで割ると、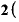 ⊿
⊿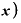 ・
・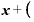 Δ
Δ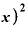 の中の「⊿x」がそれぞれ約分される。
の中の「⊿x」がそれぞれ約分される。
・その結果、「2x」(このxは、前に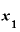 として表現していたもの)と、「⊿x」つまり「xの差」の値だけが残る。
として表現していたもの)と、「⊿x」つまり「xの差」の値だけが残る。
x=1ならば、
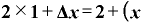 の差)
の差)
であり、x=2のときには、
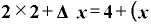 の差)
の差)
になるわけです。
xの差「⊿x」の値が極小であれば、「2x+⊿x」という値全体に占める⊿xの存在感も極小になります。
⊿xが限りなくゼロに近いくらいの微々たる値でしかなければ、「2x+⊿x」は、「ほとんど2x」と言って差し支えないくらい「2x」に限りなく近い値になるでしょう。
これが、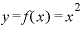 を微分して出てくる導関数が「2x」になる理由です。
を微分して出てくる導関数が「2x」になる理由です。
この「2x」の「2」という係数は、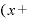 ⊿
⊿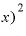 の展開式から出てきたものですから、よって、「
の展開式から出てきたものですから、よって、「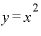 を微分すると2xになるのは、xの2乗だから」ということで正解、です。
を微分すると2xになるのは、xの2乗だから」ということで正解、です。
■一次関数を微分すると、xの係数になる■
ここで、少し戻って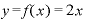 という一次関数をxで微分する、という作業をやってみましょう。
という一次関数をxで微分する、という作業をやってみましょう。
やり方は同じ、(1)の定義式に、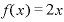 を当てはめるだけです。
を当てはめるだけです。
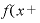 Δ
Δ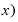 の部分は、「
の部分は、「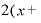 Δ
Δ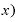 」になるので、
」になるので、
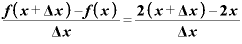
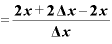
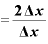
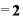
ここでもΔxが約分されて消えて、結局、2という値だけが残りました。
この計算結果にもはやΔxはありませんから、Δxが大きかろうと、小さかろうと、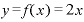 という関数を微分すれば「2」になる、すなわち
という関数を微分すれば「2」になる、すなわち

と一定です。
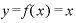 という、xに係数がついていない(というか、係数が1の)一次関数の微分の場合は、
という、xに係数がついていない(というか、係数が1の)一次関数の微分の場合は、
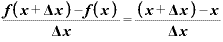
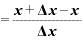
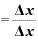
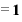
となります。
この2つの結果からわかるとおり、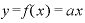 (aは定数)という形の一次関数を微分すると、その結果は、「a」というxの係数そのものになります。
(aは定数)という形の一次関数を微分すると、その結果は、「a」というxの係数そのものになります。
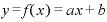 というふうに、
というふうに、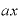 に何かの定数が足されていたり、引かれている場合でも、
に何かの定数が足されていたり、引かれている場合でも、
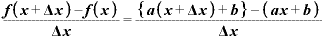
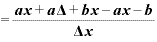
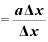
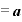
となって、「b」は差し引かれて消えてしまうため、やはり微分した結果はxの係数「a」そのものになります。 ◇