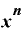 を微分すると「
を微分すると「 ・
・ 」になるのは何故?(2)
」になるのは何故?(2)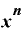 を微分すると「
を微分すると「 ・
・ 」になるのは何故?(2)
」になるのは何故?(2)
■ の微分をせっせと計算してみる■
の微分をせっせと計算してみる■
前ページで見てきた結果
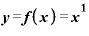 を
を で微分すると、「1」。
で微分すると、「1」。
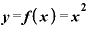 をxで微分すると、「2x」。
をxで微分すると、「2x」。
から考えると、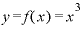 をxで微分したらどうなるか、もう予想がつくと思います。
をxで微分したらどうなるか、もう予想がつくと思います。
果たして予想通りになるかどうか、少々面倒なのですが、計算してみることにします。
まず、定義式の分子「 Δ
Δ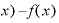 」は、
」は、
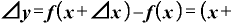 ⊿
⊿
となります。
これを計算するために、 の展開式を思い出しておきましょう。
の展開式を思い出しておきましょう。
先ほど使った の結果を活用すると、
の結果を活用すると、

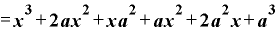

と出てきます。
この「a」の部分を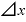 に置き換えれば、
に置き換えれば、
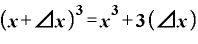 ・
・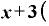 Δ
Δ ・
・ Δ
Δ
です。
そうすると、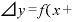 Δ
Δ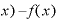 は
は
 ⊿
⊿
 Δ
Δ Δ
Δ
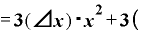 Δ
Δ Δ
Δ
となって、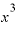 が消えてしまいました。
が消えてしまいました。
さらに、この式の各項に「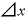 」が入っています。
」が入っています。
これを括り出してしまうと、
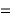 ⊿
⊿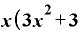 ⊿
⊿
という形にまとまります。
これが分子で、分母はΔxですから、、ここでもまたΔxが約分できます。
その結果、
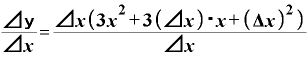
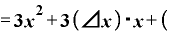 Δ
Δ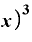
となります。
これまでやってきたのと同じように、⊿xの値をどんどん小さくしていって、それこそゼロに限りなく近いくらい微々たる値にしたとすると、この式の中の「3(⊿x)・x」は非常に小さい値になるであろうと予想できます。
ましてや、その極々微々たる⊿xを2乗した値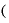 Δ
Δ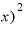 ともなれば、もはや「ゼロ」といってもいいくらいの値になるはずです。
ともなれば、もはや「ゼロ」といってもいいくらいの値になるはずです。
たとえば、⊿xが0.00001だとすると、「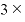 ⊿
⊿ 」の値は「0.00003」。
」の値は「0.00003」。
これにxを掛けたとすると、少なくとも「 」に比べればかなり小さい値になることは間違いありません。
」に比べればかなり小さい値になることは間違いありません。
さらに Δ
Δ となると、小数点以下が2倍増えて「0.0000000001」です。
となると、小数点以下が2倍増えて「0.0000000001」です。
とすれば、⊿xを極々微々たる値にしたときには、もう「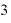 (
(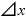 )・
)・ 」や「(
」や「(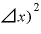 は無視できるくらいの値になって、数らしい数は「
は無視できるくらいの値になって、数らしい数は「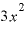 」しかない、という状況になる、と考えてもよいのではないでしょうか。
」しかない、という状況になる、と考えてもよいのではないでしょうか。
実際に、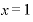 、
、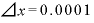 で計算してみましょう。
で計算してみましょう。
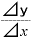 が「
が「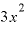 」に近い値になるとすれば、計算の結果は「
」に近い値になるとすれば、計算の結果は「 =3」に近い値になると予想されます。
=3」に近い値になると予想されます。

と、確かに、3に近い値が出てきました。
 ⊿
⊿ としたらどうでしょうか。ちなみに、xが2ならば、
としたらどうでしょうか。ちなみに、xが2ならば、 は「12」です。
は「12」です。
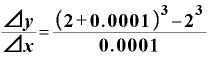



ちゃんと「12」近い値になってくれています。
⊿xをもっともっと小さい値にすれば、さらに「3」や「12」に近い値になるであろうことは想像するに難くありません。
 を微分して出てくる結果は「
を微分して出てくる結果は「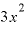 」と言ってよさそうです。
」と言ってよさそうです。
■「 のn乗」の展開式。「
のn乗」の展開式。「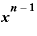 」の係数に注目■
」の係数に注目■
ここまで見てきた、 、
、 、そして
、そして と、3つの関数を微分した結果を見比べると、あるパターンが見えてきます。
と、3つの関数を微分した結果を見比べると、あるパターンが見えてきます。
繰り返しになりますが、
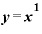 をxで微分すると「1」
をxで微分すると「1」
 をxで微分すると「
をxで微分すると「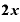 」
」
 をxで微分すると「
をxで微分すると「 」
」
です。
いずれも微分した結果は、もとの関数の「xの何乗」という指数部分の数字が前に出てきて、xの指数はもとの「何乗」の数字よりも1つ小さい値になっています。
「何乗」というのを「n乗」と表せば、「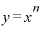 」という関数をxで微分すると、その結果は、
」という関数をxで微分すると、その結果は、
 ・
・
という形です。
まさに、かつて習った公式で、これは、n乗がいくらでも当てはまる、というのです。
このように、丸暗記で機械的にやってしまえるのは簡単・便利で嬉しいことではありますが、しかし、なぜ、そんなふうにやってしまってよいのでしょうか。
まず、nが自然数の場合ですが、これは「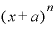 を展開すると、その展開式にはある規則性がある」ということと関係しています。
を展開すると、その展開式にはある規則性がある」ということと関係しています。
今一度、 を例に考えてみます。
を例に考えてみます。
これは、さっきも述べたとおり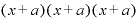 のことです。
のことです。
カッコが3つあって、それぞれのカッコの中には「x」と「a」という2つの要素が入っているわけですが、これを「展開する」とは、
①3つあるカッコそれぞれから、「x」か「a」か、どちらかを選んで、選んだ3つを掛ける
②考えられる全ての「x」と「a」の組み合わせでそれを行い、掛けて出てきたものを全部足す
という作業を意味します。具体的には、
・.3つのカッコ全てから「x」を選ぶ・・・・・・・・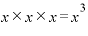
・最初のカッコから「x」、真ん中のカッコも「x」、最後のカッコは「a」・・・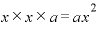
・最初のカッコから「x」、真ん中のカッコは「a」、最後のカッコは「x」・・・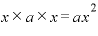
・最初のカッコから「x」、真ん中のカッコは「a」、最後のカッコも「a」・・・
・最初のカッコから「a」、真ん中のカッコは「x」、最後のカッコも「x」・・・
・最初のカッコから「a」、真ん中のカッコは「x」、最後のカッコは「a」・・・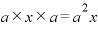
・最初のカッコから「a」、真ん中のカッコも「a」、最後のカッコは「x」・・・
・3つのカッコとも「a」を選ぶ・・・・・・・・・
という8パターンが考えられて、これらを全て足すと、
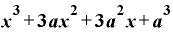
とまとまって、当然のことではありますが、さっき計算したのと同じ式になります。
またもや繰り返しになってしまいますが、「a」という文字を⊿ に置き換えれば、
に置き換えれば、
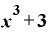 (
(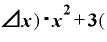 Δ
Δ Δ
Δ
です。
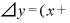 ⊿
⊿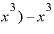 を計算すると、さっき見たように
を計算すると、さっき見たように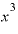 の項は差し引かれて消えて、
の項は差し引かれて消えて、
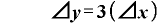 ・
・ (Δ
(Δ ・
・ Δ
Δ
だけが残ります。
これを⊿xで割ると、それぞれの項の⊿xが1つずつ約分されて消えるので、
 ・
・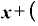 Δ
Δ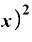
となります。
そうすると、極々微々たる値「⊿x」を含まない項は「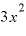 」のみになってしまいます。それが故に、
」のみになってしまいます。それが故に、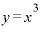 を微分すると
を微分すると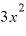 になったわけです。
になったわけです。
この結果が出てきた最大のポイントは、「 )の3乗」を展開したときに「
)の3乗」を展開したときに「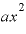 」の項の係数(
」の項の係数( であれば、「⊿
であれば、「⊿ 」の前に出てくる係数)が「3」という、もとの関数「xの3乗」の「3」と同じ値にとなったことにあります。
」の前に出てくる係数)が「3」という、もとの関数「xの3乗」の「3」と同じ値にとなったことにあります。
一体なぜ、ここに「3」なる係数が出てきたのかというと、これは、「3つあるカッコのうちの2つから『x』を選ぶ組み合わせのパターン数」だからです。
先に見たとおり、3つあるカッコのうちの2つから「x」を選ぶ組み合わせは、
・最初のカッコと真ん中のカッコからxを選ぶ
・最初のカッコと最後のカッコからxを選ぶ
・真ん中のカッコと最後のカッコからxを選ぶ
という3パターンです。
そして残り1つのカッコから「a」を取ります。それぞれ「xを2つとaを1つ」掛けて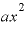 。それが3つあるから
。それが3つあるから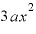 になっています。
になっています。
「3つあるカッコのうち2つから『x』を選ぶ」というのは、「3つあるカッコのどれかひとつだけ『a』を選ぶ」ということでもあります。
そうすると、カッコが3つあれば、そのうち1つだけ「a」を選ぶパターンは「最初のカッコ」か「真ん中」か「最後のカッコ」かの3つしかありません。
つまり、このパターン数はカッコの数と同じなのです。
カッコが100あればパターン数は100。カッコがn個ならば、パターン数は「n」になるわけですが、このカッコの個数「n」とは何かというと、これは「n乗」のnそのものにほかなりません。
このnが、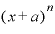 を展開したとき「
を展開したとき「 」の前にきて「
」の前にきて「 」になります。
」になります。
「a」を「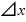 」に置き換えれば、「n・
」に置き換えれば、「n・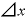 ・
・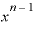 」です。
」です。
そして、この中の⊿ は分母のΔxとの約分によって消えてしまいます。
は分母のΔxとの約分によって消えてしまいます。
その結果、この項は「 」となって、
」となって、 に左右されない値と化します。
に左右されない値と化します。
これ以外の項は、約分された後にも⊿xが残るために極小の値になってしまい、ゼロと同等の扱いを余儀なくされるところとなってしまいます。
と、いうわけで、nが自然数の場合、 を微分すると、
を微分すると、
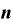 ・
・
だけが”目に見える値”として残る、というわけです。
もし、 の前に何か係数「a」がついている場合、
の前に何か係数「a」がついている場合、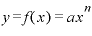 という関数であれば、それに「a」を掛けるだけ。
という関数であれば、それに「a」を掛けるだけ。
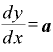 ・
・ ・
・
です。
■「マイナスn乗」でも同じ公式が使える■
この「 をxで微分すると、
をxで微分すると、 ・
・ になる」という微分計算の公式は、nが自然数でなくとも、たとえば「マイナスn乗」の場合でも同じように使えます。
になる」という微分計算の公式は、nが自然数でなくとも、たとえば「マイナスn乗」の場合でも同じように使えます。
すなわち、 という関数をxで微分すると、
という関数をxで微分すると、
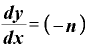 ・
・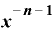
になります。
本当かどうか、ここで、再び微分の定義式により。

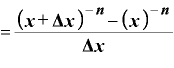 ……③
……③
を計算してみます。
まず、 とは何かというと、「0.5乗とな一体どういう意味なのか」の中に出てきた指数法則のとおり、
とは何かというと、「0.5乗とな一体どういう意味なのか」の中に出てきた指数法則のとおり、

です。
つまり、③を書き換えれば、

となります。
分子にある分数を通分してまとめると、
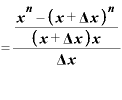

という形にできます。
ここで、まず分子に注目。これを書き換えれば、
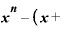 Δ
Δ Δ
Δ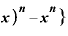
です。
これは、nが自然数のときの の微分の定義式の分子「
の微分の定義式の分子「 Δ
Δ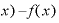 」にマイナスをつけたものと同じです。
」にマイナスをつけたものと同じです。
そこで、これを
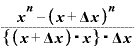
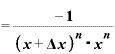 ・
・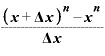
と書き換えてみれば、この式の後ろ半分は「 をxで微分したもの」と同じになります。
をxで微分したもの」と同じになります。
公式を使えば、これは、
 ・{
・{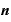 ・
・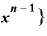
ということです。
今度は、この式の前の部分の分母に目を向けてみます。
Δxはほとんどゼロといってもいいくらいの極々わずかな値です。
とするならば、(x+Δx)は「ほとんど『x』といっても差し支えない値」として扱っていいのではないでしょうか。
この「x+Δx」を思い切って「x」としてしまえば、この式は、
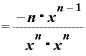
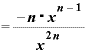
とまとまります。
分母の「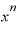 ・
・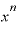 」が「
」が「 」に変わっていますが、これも「0.5乗とは一体どういう意味なのか」の中に出てきた指数法則に基づきます。
」に変わっていますが、これも「0.5乗とは一体どういう意味なのか」の中に出てきた指数法則に基づきます。
さらに、分母は「『xの2n乗』分の1」ということですから、これまた指数法則によって、

と書き換えられます。
これを用いると、
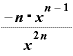
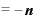 ・
・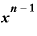 ・
・
という形にできます。
そのうえさらに、この式の「 ・
・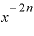 」の部分は、またもや再び指数法則によって、
」の部分は、またもや再び指数法則によって、
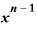 ・
・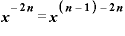
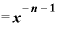
とすることができてしまいます。
その結果、この式は、
 ・
・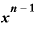 ・
・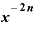
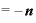 ・
・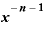
というシンプルな形になってしまうのです。
最初と途中と最後の結果をかいつまんで書けば、 という関数をxで微分した結果は、
という関数をxで微分した結果は、


 ・
・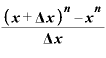
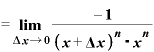 ・{
・{ ・
・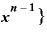 ←ここで「Δx」をゼロ同然の扱いにする。
←ここで「Δx」をゼロ同然の扱いにする。
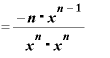 ←もはやΔxはなくなったので「lin」も不要に。
←もはやΔxはなくなったので「lin」も不要に。
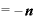 ・
・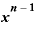 ・
・
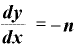 ・
・
と、見事、公式通りの形になりました。 ◇