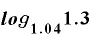 」年とは、具体的に何年なのか
」年とは、具体的に何年なのか「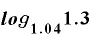 」年とは、具体的に何年なのか
」年とは、具体的に何年なのか
■指数法則を対数に変えると便利な公式ができる■
関数電卓や表計算ソフト『Excel』には、その対数がいくらになるのか、具体的な数値を出してくれる機能があります。
が、比較的手軽な関数電卓の場合には計算できる対数は、底が10の常用対数(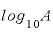 という形の対数)か、底がネイピア数eの自然対数だけです。(ネイピア数「e」については、年複利回数が大きくなると残高が定額に近づく理由とは、を見て下さい。
)
という形の対数)か、底がネイピア数eの自然対数だけです。(ネイピア数「e」については、年複利回数が大きくなると残高が定額に近づく理由とは、を見て下さい。
)
この場合、「金利4%で複利運用したとき、100万円の元本が130万円になる年数」、すなわち、底が1.04の「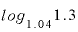 」の値を直接出すことができません。
」の値を直接出すことができません。
ただ、直接出すことはできないものの、この「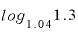 」を常用対数か自然対数に置き換えれば、間接的に計算することは可能です。
」を常用対数か自然対数に置き換えれば、間接的に計算することは可能です。
もちろん、Excelを使えば、底がいくらの対数でもすぐに計算できます(具体的なやり方は、Excelで対数の値を計算してみる、をご覧下さい。)。
が、ここでは、あえて「常用対数か自然対数しか計算できないとき」の計算のやり方を紹介します。
というのは、高校数学の公式集などでは、「真数がいくらのとき、常用対数の値はいくらになるか」をまとめている常用対数表がついていて、この表の値を調べれば、関数電卓さえも使わずに、底がいくらの対数でも、その値を知ることができるからです。
そのために、まずは、かつて習った対数の公式を思い出しておきます。
この対数の公式は、、「0.5乗とは一体どういう意味か」で出てきた指数法則から考えると、その意味がすぐにわかると思います。
(対数の公式その1)……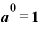 の変形
の変形
底がいくらであっても、真数が1ならば、その対数の値は0
指数法則
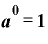
を「aは何乗すると1になるか」という対数に書き換えると、
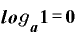
です。
どんな数も「ゼロ乗」は「1」、底がいくらであっても、真数が「1」の対数は「ゼロ」になります。
(対数の公式その2)……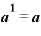 の変形
の変形
底と真数が同じ対数の値は「1」である。
たとえば、底が2、真数も2という対数「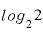 」とは、「(底の)2が(真数の)2にするには何乗すればいいか」という意味です。
」とは、「(底の)2が(真数の)2にするには何乗すればいいか」という意味です。
どんな数も「1乗」した結果は、その数自身と同じです。
底と真数をaとすれば、
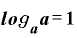
です。
これを少し発展させて、たとえば真数が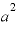 の場合はどうなるかというと、もともと対数の値は「底の値を何乗すると真数になるのか」ですから、底が
の場合はどうなるかというと、もともと対数の値は「底の値を何乗すると真数になるのか」ですから、底が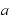 で、真数が
で、真数が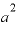 ならば、対数の値は「2」。真数が
ならば、対数の値は「2」。真数が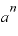 ならば、対数の値は「n」です。
ならば、対数の値は「n」です。
つまり、
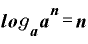
というわけです。
(対数の公式その3)
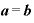 のとき、底が同じで真数がそれぞれa、bの対数もやはり等しい。
のとき、底が同じで真数がそれぞれa、bの対数もやはり等しい。
たとえば、aもbも「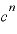 」で表される同じ値だとします(cは0より大きく、1でない実数)。
」で表される同じ値だとします(cは0より大きく、1でない実数)。
すなわち、
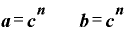
です。
この「n乗」を対数で表現すると、
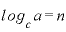
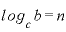
と、どちらの値もnになります。よって、
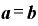 ならば
ならば 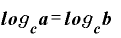
が成り立ちます。
たとえばaなり、bなりのある値があって、それを真数とした対数にすることを「対数をとる」などと呼ばれます。
2つの値の間で等式が成り立っていれば、両辺対数を取ってもやはり等式が成り立ちます。
いかにも当たり前な感じですが、実はこの先、この公式が非常に重要になります。
(対数の公式その4)
真数が「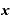 ×
×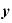 ]というような掛け算になっている対数は、底が同じ値の対数の足し算にすることができる。
]というような掛け算になっている対数は、底が同じ値の対数の足し算にすることができる。
底が「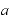 」の対数でこれを式で表現すると、、
」の対数でこれを式で表現すると、、
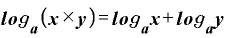
という形になる、という公式です。
これは、指数関数の「掛け算を足し算にすることができる」法則
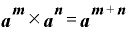
から説明されます。
たとえば、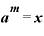 で。
で。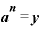 だとします。そうすると「
だとします。そうすると「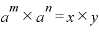 」ですから、上の指数法則は、
」ですから、上の指数法則は、
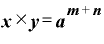
と表現できます。
ここで、両辺について「a」を底とする対数を取ってみます。
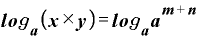
ですが、対数の公式その2で出てきた、「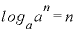 」を用いると、
」を用いると、
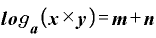 ……(A)
……(A)
になります。
一方、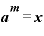 と
と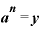 を、それぞれaを底とした対数にすると、
を、それぞれaを底とした対数にすると、
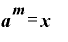 →
→ 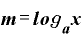
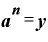 →
→ 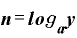
です。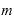 は「
は「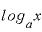 」であり、
」であり、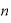 は「
は「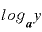 」で表現できるわけです。
」で表現できるわけです。
これを、先ほどの{A}式に取り入れると、
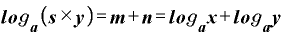
と、最初に登場した公式になります。
もし、左辺の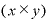 の部分が
の部分が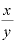 という分数だったらどうなるでしょうか。
という分数だったらどうなるでしょうか。
これもやはり指数法則
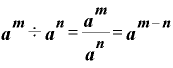
との関連で考えることができます。
ここでも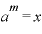 、
、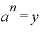 とすると、「
とすると、「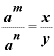 」となりますから、上の指数法則は、
」となりますから、上の指数法則は、
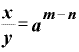
になり、両辺ともaを底とする対数にすると、
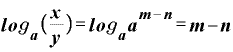 ……(B)
……(B)
です。
先ほどと同じく、mは「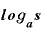 」であり、nは「
」であり、nは「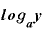 」ですから、これをに(B)式に取り入れると、
」ですから、これをに(B)式に取り入れると、
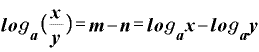
という形になります。
そこで
(対数の公式その5)
真数が「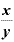 ]というような割り算になっている対数は、底が同じ値の対数の引き算にすることができる。
]というような割り算になっている対数は、底が同じ値の対数の引き算にすることができる。
ということになります。
(対数の公式その6)
真数が「n乗」という形になっている場合、真数から「n乗」を取り外した対数と「n」の掛け算にすることができる。
底をa,真数をbとした対数でこれを表現すると、
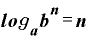 ・
・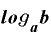
真数bから「n乗」を取ってしまい、「n」だけを前に出せる、という公式です。
これは、「aのm乗をさらにn乗すると、aの(m×n)乗になる」という指数法則
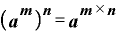
から説明することができます。
まず、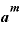 が「b」という値だとします。
が「b」という値だとします。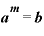 ですから、上の指数法則に当てはめれば、
ですから、上の指数法則に当てはめれば、
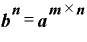
です。
ここで両辺、aを底とした対数を取ってみます。
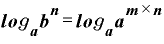
ですが、今回も左辺は対数の公式その2によって、
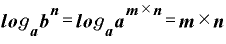 ……(C)
……(C)
とすることができます。
一方、「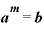 」から「m」を対数で表現すると、
」から「m」を対数で表現すると、
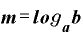
です。
このmの表現を(C)式に取り入れると、
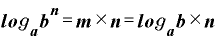
となり、「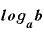 」と「n」の掛け算になる、という公式が出てきます。
」と「n」の掛け算になる、という公式が出てきます。
(対数の公式その7)
「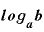 」という対数は、「
」という対数は、「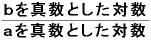 」(分母、分子の対数の底は同じ値で、0より大きく、1でない数)という分数に変換できる。
」(分母、分子の対数の底は同じ値で、0より大きく、1でない数)という分数に変換できる。
たとえば、「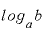 」を取りあえずkなどという適当な値に置き換えます。つまり、
」を取りあえずkなどという適当な値に置き換えます。つまり、
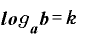 →
→ 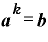
です。
この「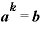 」の両辺について、「c」を底とする対数を取ってみます。
」の両辺について、「c」を底とする対数を取ってみます。
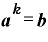
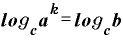
ここで、右辺の「k乗」は対数の公式その6によって前に出すことができます。
すなわち、
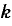 ・
・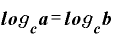
になります。
これを変形すると、
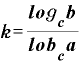
ですが、「k」は「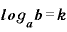 」ということでしたから、これは結局、
」ということでしたから、これは結局、
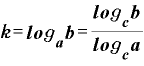
となって、これが公式その7です。
公式が長くなってしまいましたが、「金利4%のときに、元本が1.3倍になる年数」を表す対数「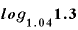 」の具体的な値を計算するときには、この公式その7を使いますす。
」の具体的な値を計算するときには、この公式その7を使いますす。
■「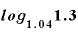 」を底が10の常用対数に変換する■
」を底が10の常用対数に変換する■
「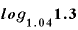 」という対数は、「公式その7」があれば、常用対数でも自然対数でも、どちらにも簡単に変換できます。
」という対数は、「公式その7」があれば、常用対数でも自然対数でも、どちらにも簡単に変換できます。
公式その7の右辺の底「c」のところに、常用対数ならば「10」、自然対数なら「e」を当てはめれば、分母と分子の具体的な値が特定できます。あとは、割り算をするだけです。
ここでは、底が10の常用対数に変換してみましょう(自然対数に変換しても、答えはもちろん同じです)。
公式その7を使うと、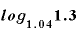 は、
は、
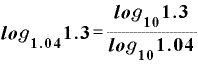
という分数になります。
分母・分子それぞれを関数電卓で計算すると、
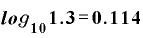
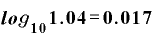
という値が出てきます。
これを割り算すると、「金利4%のとき、元本が1.3倍になる年数」は
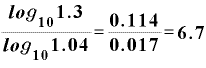 (年)
(年)
と出てきました。
■金利5%の複利運用で元本が2倍になる年数は?■
同じようなやり方で、本文の(2)で出てきた「金利が5%のとき、元利が2倍になる年数」が計算できます。
元本が2倍になる年数Tを表す対数は、
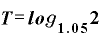
です。
これを先ほどと同じように常用対数の形にすれば、
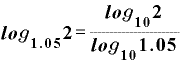
となります。
分母・分子を関数電卓で計算すると、
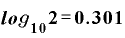
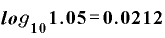
よって、元本が2倍になる年数Tは、
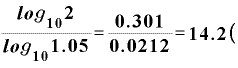 年)
年)
です。 ◇