
乮侾乯栚昗偺尦棙崌寁妟偵摓払偡傞擭悢傪媮傔傞偵偼
暋棙塣梡偱偒傞嬥梈彜昳偑偁傞偲偒丄傑偢峫偊傞偺偼乽偙偺嬥棙偱枮婜傑偱塣梡偟偨傜丄尦棙崌寁妟偼偄偔傜偵側傞偐乿偱偼側偄偐偲巚偄傑偡丅
擭侾夞暋棙偺応崌側傜丄尦杮傪俹侽丄嬥棙傪倰偲偡傞偲丄俿擭屻偺尦棙崌寁妟俹偼丄

偱寁嶼偱偒傑偡丅
偙偺寁嶼偼丄尦杮偲塣梡嬥棙丄偦偟偰擭悢偑梊傔傢偐偭偰偄偰丄偦偙偐傜尦棙崌寁妟傪媮傔偰偄傞傢偗偱偡偑丄嬥梈彜昳傪慖傇偲偒偵偼乽偄傑偁傞尦杮傪仜擭屻偵偄偔傜偵憹傗偟偨偄丅偦傟偵偼擭壗亾偁傟偽偄偄偺偐乿偲峫偊傞働乕僗傕偁傞偱偟傚偆丅偮傑傝丄尦杮偲尦棙崌寁偺栚昗妟丄偦偟偰塣梡擭悢偑寛傑偭偰偄偰丄偦傟傪幚尰偡傞偺偵昁梫側嬥棙傪媮傔偨偄丄偲偄偆働乕僗偱偡丅
偙偺応崌偼丄愭傎偳偺乽尦棙崌寁妟俹亖乿偺幃傪乽嬥棙倰亖乿偲偄偆宍偵曄宍偡傟偽弌偰偒傑偡丅偡側傢偪丄
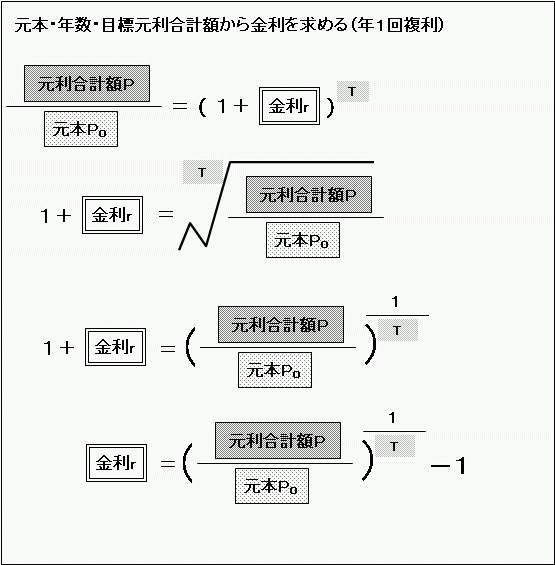
偲側傝傑偡丅
仸乽俿忔崻乿偑側偤乽俿暘偺侾忔乿偵丠丠丠丂偲偄偆曽偼丄乽侽丏俆忔乿偲偼堦懱偳偆偄偆堄枴側偺偐丄傪尒偰壓偝偄丅
偝傜偵丄偙傫側傆偆偵峫偊傞偙偲傕偁傞偲巚偄傑偡丅
乽偙偺嬥棙偱暋棙塣梡偟偨応崌丄尦棙崌寁偑栚昗妟偵摓払偡傞傑偱偵壗擭偐偐傞偺偐乿丅
偮傑傝丄尦杮偲塣梡嬥棙丄偦偟偰栚昗偺尦棙崌寁妟偑嵟弶偵寛傑偭偰偄偰丄偦傟傪幚尰偡傞偺偵昁梫側擭悢傪媮傔偨偄働乕僗偱偡丅
偙傟偼丄乽侾亄嬥棙倰乿傪俿忔偡傞応崌偺巜悢晹暘乽俿乿傪媮傔傞偲偄偆偙偲偱偡丅偳偆傗偭偰媮傔傟偽偄偄偺偐偲偄偆偲丄偙偆偟偨偲偒偵搊応偡傞偺偑丄崅峑偺悢嘦偱廗偭偨懳悢丄偁偺乽log乿側傞傕偺偱偡丅
偨偲偊偽丄乽俀傪値忔偡傞偲俉偵側傞乿偲偄偆幃偼乽俀値亖俉乿偱偡丅偙傟傪乽俀傪俉偵側傜偟傔傞偺偼丄値偲偄偆巜悢偱偁傞乿偲偄偆傆偆偵丄値忔偺乽値乿傪昞尰偡傞偲偒偵偼乽値亖log 2 俉乿偲偟傑偡丅
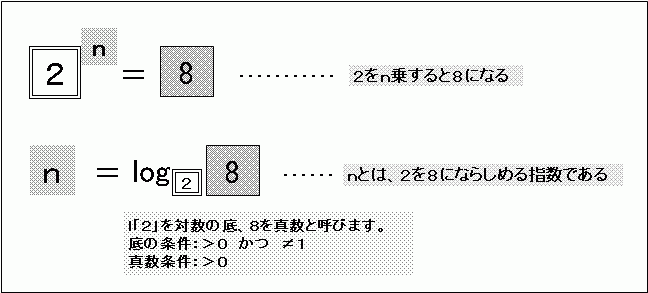
偙偺応崌丄値偼俁偱偡丅
仸乽懳悢乿側傞傕偺偲偼偳傫側傕偺偩偭偨偐側丠丄偲偄偆曽偼丄log偲偼壗傪昞尰偡傞傕偺側偺偐丄傪偛棗壓偝偄丅
偙傟偲摨偠傛偆偵偡傟偽乽擭悢俿乿偑昞尰偱偒傑偡丅
偙偙偱丄俿忔偡傞乽侾亄嬥棙倰乿傪乽俼乿偲偄偆侾暥帤偵偟偰偟傑偄傑偡丅嬥棙偑係亾丄偮傑傝倰偑0.04側傜偽丄俼偼1.04丅偲偄偭偨嬶崌偵丄嬥棙倰偑梊傔寛傑偭偰偄傟偽帺摦揑偵俼傕寛傑傝傑偡偐傜丄栤戣偼偁傝傑偣傫丅
尦杮傪俹侽丄栚昗偺尦棙崌寁妟傪俹偲偡傞偲丄擭悢俿偼丄
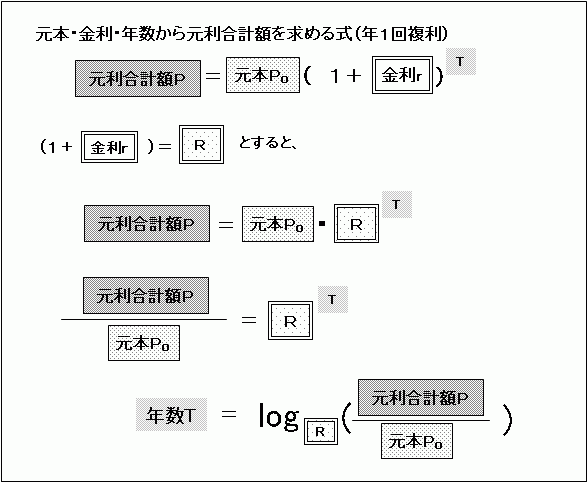
偲偄偆幃偱媮傔傜傟傑偡丅
偨偲偊偽丄尦杮侾侽侽枩墌偼嬥棙係亾偱壗擭暋棙塣梡偡傞偲侾俁侽枩墌偵側傞偺偐丄偲偄偆応崌側傜偽丄
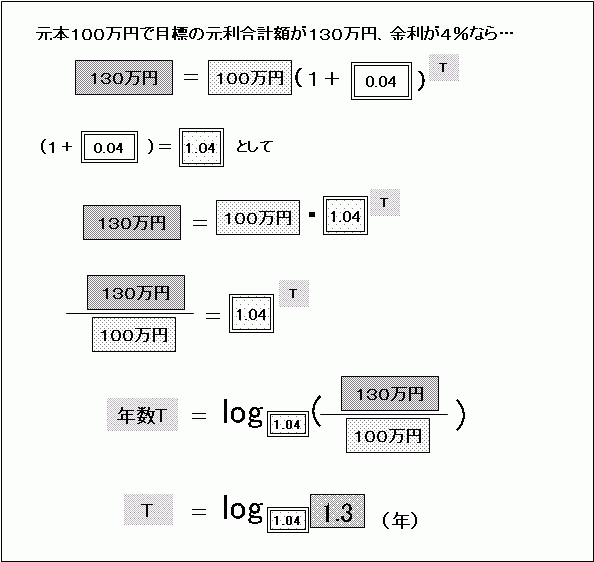
偱偡丅
偙偺 log 1.041.3 偲偄偆幃偱偡偑丄掙偺1.04傕恀悢1.3傕梊傔寛傑偭偰偄傞悢側偺偱丄偙偺幃偺抣偼傕偼傗摿掕偝傟傑偡丅
偱偡偐傜丄乽嬥棙係亾偺暋棙塣梡偱尦杮侾侽侽枩墌偑尦棙崌寁侾俁侽枩墌偵側傞偺偼壗擭屻偐乿偲偄偆栤戣傪弌偝傟偨偲偒偵丄乽log 1.041.3 擭偱偡乿偲摎偊偰傕娫堘偄偱偼偁傝傑偣傫丅
偙傟偼丄乽嬥棙係亾偱擭侾夞暋棙塣梡偟偨傜丄尦杮侾侽侽枩墌偼俆擭屻偵偄偔傜偵側傞偐乿偲偄偆栤戣偵懳偟偰丄乽1.04俆亊侾侽侽枩墌偱偡乿偲摎偊傞偺偲摨偠傛偆側偙偲偱偡丅
偲偼偄偊丄乽昁梫側擭悢偼亀log 1.041.3亁擭偩乿側偳偲尵傢傟偰傕丄嬶懱揑偵壗擭側偺偐丄偙傟偱偼僀儊乕僕偡傜偱偒傑偣傫丅
偙偺幃偺抣偑晛抜巊偭偰偄傞悢抣偵偡傞偲壗擭偵側傞偺偐偼丄娭悢揹戩傗亀俤倶們倕倢亁偱寁嶼偡傞偙偲偑偱偒傑偡丅
嬶懱揑側擭悢偼6.7擭偱偡丅
仸嬶懱揑側寁嶼曽朄傪抦偭偰偍偒偨偄偲偄偆曽偼丄乽log1.041.3乿擭偲偼丄嬶懱揑偵壗擭側偺偐丄傪偛棗壓偝偄丅
仾 Top 傊栠傞丅