(2)マイナス複利運用で考える「半減期」
元利合計目標額を「元本の2倍」としてみましょう。
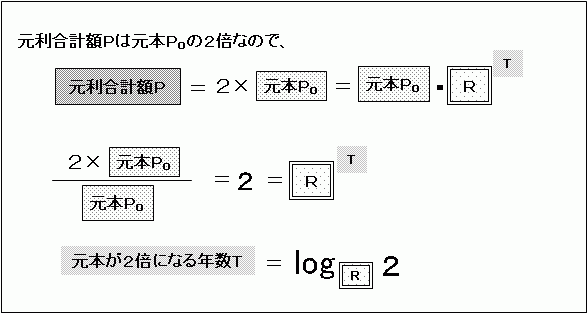
元本をP0とすると、元利合計額Pは元本の2倍ですから「P=2P0」です。
先ほどと同じように、「1+金利r」を「R」とすれば、

となります。
たとえば、金利が5%の場合、R=1.05。これを上の式に代入すると、金利5%で元本が2倍になる年数は、log 1.05 2年です。この log 1.05 2 を計算すると、14.2 年。金利5%で年1回複利運用すると、14 年少々で元本は2倍に増える、というわけです。
※log 1.05 2 がなぜ 14.2 になるのか、興味がある方は、「log1.041.3」年とは、具体的に何年なのか、をご覧下さい。
金利と「元本が2倍に増える年数」の関係については、マネー関係の記述などで「72の法則」が紹介されることがあります。元本が2倍になるのは「金利×年数」がおよそ72になる、というもので、金利が5%なら、「5(%)×年数=72」となって、14年と出てきます。確かに、計算した値14.2年とほぼ一致します。
ただ、この「72の法則」はどんな金利水準でも当てはまるわけではありません。
図表1は、金利を0.01%から12%まで変えて、元本が2倍になる年数を計算した結果です。
図表1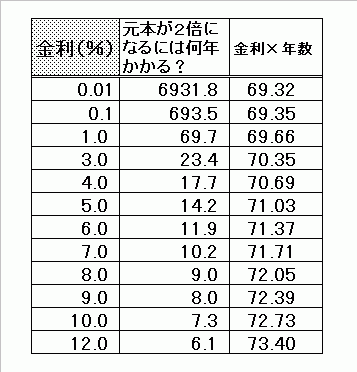
金利が高くなると「金利×元本が2倍になる年数」の値も大きくなっていきます。掛け算の結果が72近辺になるのは、概ね金利4%〜10%の範囲です。
この範囲辺りの値が「通常の金利水準」であり、その水準においては金利と年数を掛け算した結果がおよそ72になる、ということで、この「72の法則」がどんな指数関数に当てはまるわけではありません。
ちなみに、金利と元本が2倍になるために必要な年数の関係をグラフにすると、図表2のようになります。
金利がゼロに近いほど必要年数は非常に大きな値になり、金利1%辺りから必要年数は徐々に短くなっていくことがわかります。
図表2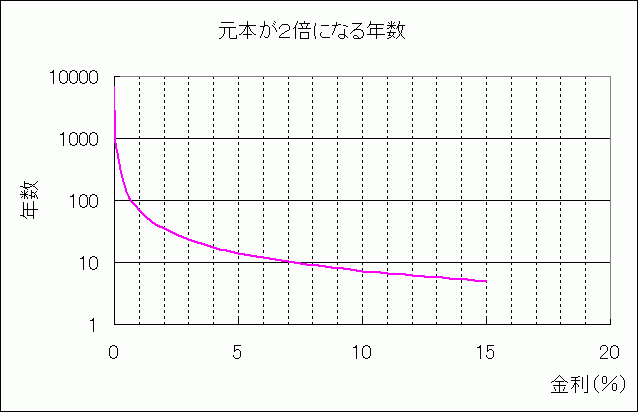
※金利がゼロに近いと年数が非常に大きくなるため、縦軸は対数にしてあります。「対数グラフ」については、こんなときには「対数グラフ」が見やすい、をご覧下さい。
ところで、金利が複利で元本を増やしてくれる計算をしてきましたが、マイナス運用を複利的に続けていけば、当然ながら元本はどんどん減っていきます。
昨今、福島原発からの放射性物質の飛散に関連して、「ヨウ素131の半減期は8日だ」等々、半減期という言葉がニュースなどにしばしば出てきますが、ここで、“マイナス複利運用”や複利的な元金の取り崩しによって資産が半分になる「半減期」を計算してみましょう。
考え方は「元本が2倍になる年数」のときとほとんど同じですが、マイナス運用なので、(RT)にマイナスをつけます。また、「P/P0=2」であったところを、「P/P0=1/2」にします。
マイナス5%で複利運用すると、
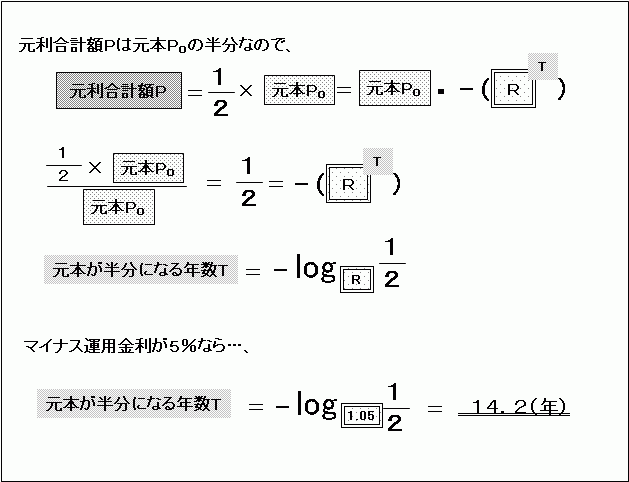
で、14.2年で元本は半分になります。ということは、元本が2倍になる年数と同じです。
他の金利で計算しても同様、マイナス複利運用したときの「半減期」は、元本が2倍になる年数と同じなのです。
※「なぜ?」という方は、「元本が2倍になる年数」=「元本が半減する年数」の理由、をご覧下さい。
運用にかかる現実のコストを考えれば、計算上の「半減期」よりももっと短い年数で資産が半減する可能性があります。
たとえば、投資信託では購入時にかかる販売手数料のほかに、信託報酬という、投資対象の資産額から毎年定率で差し引かれるコストがあります。
信託報酬が年3.5%とすると、運用が年マイナス3.5%という水準であっても、トータルで年7%のマイナス複利運用になります。これを上の式に入れてみると、10年少々で投資対象の資産額が半減する計算になります。
他方、資産の運用が仮に年10%という高実績をあげたとしても、年3.5%のコストを差し引くと年6.5%ですから、投資対象の元本が2倍になるまでに11年かかります。
見た目には大きくなさそうな運用コストも積み重なれば無視できないマイナス要因になります。十分気をつけましょう。
※金利や債券には関係ありませんが、放射性物質の半減期について興味がある方は、「半減期」の超基礎知識、をご覧下さい。
↑ Top へ戻る。